Advertisements
Advertisements
प्रश्न
The radius of a gold nucleus (Z = 79) is about 7.0 × 10-10 m. Assume that the positive charge is distributed uniformly throughout the nuclear volume. Find the strength of the electric field at (a) the surface of the nucleus and (b) at the middle point of a radius. Remembering that gold is a conductor, is it justified to assume that the positive charge is uniformly distributed over the entire volume of the nucleus and does not come to the outer surface?
उत्तर
Given:
Atomic number of gold = 79
Charge on the gold nucleus, Q = 79 × (1.6 ×10-19) C The charge is distributed across the entire volume. So, using Gauss's Law, we get:
(a) `phi =oint vec"E". vec("d""s") = "Q"/∈_0`
`=> oint "E""d""s" = "Q"/∈_0`
The value of E is fixed for a particular radius.
`=> "E" oint "d""s" = "Q"/∈_0`
`=> "E" xx 4 pi "r"^2 ="Q"/∈_0`
`=> "E" ="Q"/(∈_0 xx 4 pi "r"^2)`
`"E" = ( 79 xx (1.6 xx 10^-19 ))/((8.85 xx 10^-12) xx 4 xx 3.14 xx ( 7 xx 10^-10)^2`
`"E" = 2.315131 xx 10^21 "N"//"C"`
(b) To find the electric field at the middle point of the radius:
Radius , `"r" = 7/2 xx 10^-10 m`
Volume, `"V" = 4/3 pi "r"^3`
`=4/3 xx 22/7 xx 343/8 xx 10^-30`
Net charge =79 ×1.6 ×10-19 C
Volume charge density
`= (79 xx 1.6 xx 10^-19)/(4/3pi xx 343 xx 10^-30) `
So, the charge enclosed by this imaginary sphere of radius r =3.5× 10 -10
`= (79 xx 1.6 xx 10^-19)/(4/3pi xx 343 xx 10^-30) xx 4/3 pi xx 343/8 xx 10^-30 `
`= (79 xx 1.6 xx 10^-19)/8`
`=> "E" = (79 x 1.6 xx 10^-19)/(8 xx4pi ∈_0."r"^2)` at r = 3.5× 10-10
= 1.16 × 1021 N/C.
As electric charge is given to a conductor, it gets distributed on its surface. But nucleons are bound by the strong force inside the nucleus. Thus, the nuclear charge does not come out and reside on the surface of the conductor. Thus, the charge can be assumed to be uniformly distributed in the entire volume of the nucleus.
APPEARS IN
संबंधित प्रश्न
Plot a graph showing the variation of resistivity of a conductor with temperature.
A charge Q is uniformly distributed over a large plastic plate. The electric field at a point P close to the centre of the plate is 10 V m−1. If the plastic plate is replaced by a copper plate of the same geometrical dimensions and carrying the same charge Q, the electric field at the point P will become
A charge Q is uniformly distributed over a rod of length l. Consider a hypothetical cube of edge l with the centre of the cube at one end of the rod. Find the minimum possible flux of the electric field through the entire surface of the cube.
The electric field in a region is given by
`vec"E"= 3/5"E"_0 vec"i" + 4/5 "E"_0 vec "i" "with" " E"_0 = 2.0 xx 10^3 "N""C"^-1.`
Find the flux of this field through a rectangular surface of area 0⋅2 m2 parallel to the y-z plane.
The electric field in a region is given by `vec"E" = ("E"_0 "x")/"l" vec"i".`
Find the charge contained inside the cubical volume bound by the surfaces
x =0, x =a, y=0, y=a, z=0 and z=a. Take
`"E"_0 = 5 xx 10^3 "N""C"^-1 , "l" =2 "cm" " and" " a" = 1 "cm" `
Consider the following very rough model of a beryllium atom. The nucleus has four protons and four neutrons confined to a small volume of radius 10−15 m. The two 1 selectrons make a spherical charge cloud at an average distance of 1⋅3 ×10−11 m from the nucleus, whereas the two 2 s electrons make another spherical cloud at an average distance of 5⋅2 × 10−11 m from the nucleus. Find three electric fields at (a) a point just inside the 1 s cloud and (b) a point just inside the 2 s cloud.
A charged particle with a charge of −2⋅0 × 10−6 C is placed close to a non-conducting plate with a surface charge density of 4.0 × 10-6Cm0-2. Find the force of attraction between the particle and the plate.
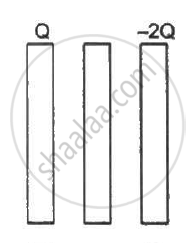
Three identical metal plates with large surface areas are kept parallel to each other as shown in the following figure. The leftmost plate is given a charge Q, the rightmost a charge −2Q and the middle one is kept neutral. Find the charge appearing on the outer surface of the rightmost plate.
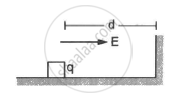
A block of mass containing a net positive charge q is placed on a smooth horizontal table which terminates in a vertical wall as shown in the figure. The distance of the block from the wall is d. A horizontal electric field E towards the right is switched on. Assuming elastic collisions (if any), find the time period of the resulting oscillatory motion. Is it a simple harmonic motion?
A uniform electric field of 10 N C−1 exists in the vertically downward direction. Find the increase in the electric potential as one goes up through a height of 50 cm.
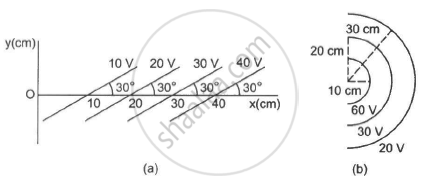
Some equipotential surface is shown in the figure. What can you say about the magnitude and the direction of the electric field?
Consider a circular ring of radius r, uniformly charged with linear charge density λ. Find the electric potential at a point on the axis at a distance x from the centre of the ring. Using this expression for the potential, find the electric field at this point.
A uniform field of 2.0 NC−1 exists in space in the x-direction. (a) Taking the potential at the origin to be zero, write an expression for the potential at a general point (x, y, z). (b) At which point, the potential is 25 V? (c) If the potential at the origin is taken to be 100 V, what will be the expression for the potential at a general point? (d) What will be the potential at the origin if the potential at infinity is taken to be zero? Is it practical to choose the potential at infinity to be zero?
Answer the following question.
Prove that the average energy density of the oscillating electric field is equal to that of the oscillating magnetic field.
Two charged conducting spheres of radii a and b are connected to each other by a wire. Find the ratio of the electric fields at their surfaces.
