Advertisements
Advertisements
प्रश्न
A uniform field of 2.0 NC−1 exists in space in the x-direction. (a) Taking the potential at the origin to be zero, write an expression for the potential at a general point (x, y, z). (b) At which point, the potential is 25 V? (c) If the potential at the origin is taken to be 100 V, what will be the expression for the potential at a general point? (d) What will be the potential at the origin if the potential at infinity is taken to be zero? Is it practical to choose the potential at infinity to be zero?
उत्तर
(a) Given:
Electric field intensity, E = 2 N/C in the x-direction
(a) Potential at the origin = 0
\[V = - E . r\]
\[ = - \left( E_x \hat{i}+ E_y \hat{j }+ E_z \hat{k} \right) . \left( x \hat{i} + y \hat{j } + z \hat{k } \right)\]
\[ \Rightarrow V = - E_x . x = - 2x\]
(b) From the above expression for V, we have
\[(25 - 0) = - 2x\]
\[ \Rightarrow x = \frac{25}{- 2} = - 12 . 5 \] m
(c) If potential at the origin is 100 V, then potential at a general point is given by
\[V - 100 = - 2x\]
\[ \Rightarrow V = 100 - 2x\]
(d) Potential at infinity is given by \[V' - V = - 2x, \]
where V is the potential at the origin.
\[\because V' = 0 , x = \infty , \]
\[V = V' + 2x = \infty\]
It is not practical to take the potential at infinity to be zero because in that case, we have to take the potential at origin to be infinity and the calculations will become practically impossible.789
APPEARS IN
संबंधित प्रश्न
plot a graph showing the variation of current density (j) versus the electric field (E) for two conductors of different materials. What information from this plot regarding the properties of the conducting material, can be obtained which can be used to select suitable materials for use in making (i) standard resistance and (ii) connecting wires in electric circuits?
A metallic particle with no net charge is placed near a finite metal plate carrying a positive charge. The electric force on the particle will be
A charge Q is uniformly distributed over a rod of length l. Consider a hypothetical cube of edge l with the centre of the cube at one end of the rod. Find the minimum possible flux of the electric field through the entire surface of the cube.
The electric field in a region is given by
`vec"E"= 3/5"E"_0 vec"i" + 4/5 "E"_0 vec "i" "with" " E"_0 = 2.0 xx 10^3 "N""C"^-1.`
Find the flux of this field through a rectangular surface of area 0⋅2 m2 parallel to the y-z plane.
The radius of a gold nucleus (Z = 79) is about 7.0 × 10-10 m. Assume that the positive charge is distributed uniformly throughout the nuclear volume. Find the strength of the electric field at (a) the surface of the nucleus and (b) at the middle point of a radius. Remembering that gold is a conductor, is it justified to assume that the positive charge is uniformly distributed over the entire volume of the nucleus and does not come to the outer surface?
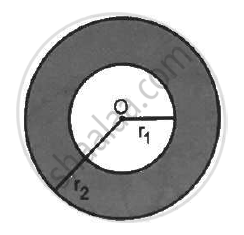
A charge Q is distributed uniformly within the material of a hollow sphere of inner and outer radii r1 and r2 (see the figure). Find the electric field at a point P at a distance x away from the centre for r1 < x < r. Draw a rough graph showing the electric field as a function of x for 0 < x < 2r2 (see the figure).
Consider the following very rough model of a beryllium atom. The nucleus has four protons and four neutrons confined to a small volume of radius 10−15 m. The two 1 selectrons make a spherical charge cloud at an average distance of 1⋅3 ×10−11 m from the nucleus, whereas the two 2 s electrons make another spherical cloud at an average distance of 5⋅2 × 10−11 m from the nucleus. Find three electric fields at (a) a point just inside the 1 s cloud and (b) a point just inside the 2 s cloud.
A charged particle with a charge of −2⋅0 × 10−6 C is placed close to a non-conducting plate with a surface charge density of 4.0 × 10-6Cm0-2. Find the force of attraction between the particle and the plate.
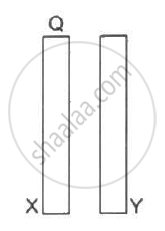
Two conducting plates X and Y, each with a large surface area A (on one side), are placed parallel to each other, as shown in the following figure . Plate X is given a charge Q,whereas the other is kept neutral. Find (a) the surface charge density at the inner surface of plate X (b) the electric field at a point to the left of the plates (c) the electric field at a point in between the plates and (d) the electric field at a point to the right of the plates.
Draw equipotential surfaces corresponding to a uniform electric field in the z-directions.
Electric field at a point is defined as ______.
The force per unit charge is known as ______.
