Advertisements
Advertisements
प्रश्न
A uniform field of 2.0 NC−1 exists in space in the x-direction. (a) Taking the potential at the origin to be zero, write an expression for the potential at a general point (x, y, z). (b) At which point, the potential is 25 V? (c) If the potential at the origin is taken to be 100 V, what will be the expression for the potential at a general point? (d) What will be the potential at the origin if the potential at infinity is taken to be zero? Is it practical to choose the potential at infinity to be zero?
उत्तर
(a) Given:
Electric field intensity, E = 2 N/C in the x-direction
(a) Potential at the origin = 0
\[V = - E . r\]
\[ = - \left( E_x \hat{i}+ E_y \hat{j }+ E_z \hat{k} \right) . \left( x \hat{i} + y \hat{j } + z \hat{k } \right)\]
\[ \Rightarrow V = - E_x . x = - 2x\]
(b) From the above expression for V, we have
\[(25 - 0) = - 2x\]
\[ \Rightarrow x = \frac{25}{- 2} = - 12 . 5 \] m
(c) If potential at the origin is 100 V, then potential at a general point is given by
\[V - 100 = - 2x\]
\[ \Rightarrow V = 100 - 2x\]
(d) Potential at infinity is given by \[V' - V = - 2x, \]
where V is the potential at the origin.
\[\because V' = 0 , x = \infty , \]
\[V = V' + 2x = \infty\]
It is not practical to take the potential at infinity to be zero because in that case, we have to take the potential at origin to be infinity and the calculations will become practically impossible.789
APPEARS IN
संबंधित प्रश्न
(i) If two similar large plates, each of area A having surface charge densities +σ and –σ are separated by a distance d in air, find the expressions for
(a) field at points between the two plates and on outer side of the plates. Specify the direction of the field in each case.
(b) the potential difference between the plates.
(c) the capacitance of the capacitor so formed.
(ii) Two metallic spheres of Radii R and 2R are charged so that both of these have same surface charge density σ. If they are connected to each other with a conducting wire, inn which direction will the charge flow and why?
Plot a graph showing the variation of resistivity of a conductor with temperature.
A charge Q is uniformly distributed over a large plastic plate. The electric field at a point P close to the centre of the plate is 10 V m−1. If the plastic plate is replaced by a copper plate of the same geometrical dimensions and carrying the same charge Q, the electric field at the point P will become
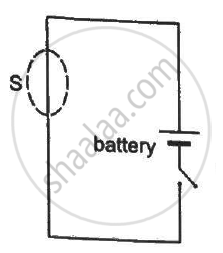
A closed surface S is constructed around a conducting wire connected to a battery and a switch in the following figure. As the switch is closed, the free electrons in the wire start moving along the wire. In any time interval, the number of electrons entering the closed surface S is equal to the number of electrons leaving it. On closing the switch, the flux of the electric field through the closed surface
(a) is increased
(b) is decreased
(c) remains unchanged
(d) remains zero
The electric field in a region is given by
`vec"E"= 3/5"E"_0 vec"i" + 4/5 "E"_0 vec "i" "with" " E"_0 = 2.0 xx 10^3 "N""C"^-1.`
Find the flux of this field through a rectangular surface of area 0⋅2 m2 parallel to the y-z plane.
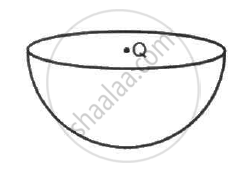
A charge Q is placed at the centre of an imaginary hemispherical surface. Using symmetry arguments and Gauss's Law, find the flux of the electric field due to this charge through the surface of the hemisphere in the following figure.
The radius of a gold nucleus (Z = 79) is about 7.0 × 10-10 m. Assume that the positive charge is distributed uniformly throughout the nuclear volume. Find the strength of the electric field at (a) the surface of the nucleus and (b) at the middle point of a radius. Remembering that gold is a conductor, is it justified to assume that the positive charge is uniformly distributed over the entire volume of the nucleus and does not come to the outer surface?
Consider the following very rough model of a beryllium atom. The nucleus has four protons and four neutrons confined to a small volume of radius 10−15 m. The two 1 selectrons make a spherical charge cloud at an average distance of 1⋅3 ×10−11 m from the nucleus, whereas the two 2 s electrons make another spherical cloud at an average distance of 5⋅2 × 10−11 m from the nucleus. Find three electric fields at (a) a point just inside the 1 s cloud and (b) a point just inside the 2 s cloud.
Find the magnitude of the electric field at a point 4 cm away from a line charge of density 2 × 10-6 Cm-1.
A non-conducting sheet of large surface area and thickness d contains a uniform charge distribution of density ρ. Find the electric field at a point P inside the plate, at a distance x from the central plane. Draw a qualitative graph of E against x for 0 < x < d.
One end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and a charge of 4.0× 10-6 C. In equilibrium, the thread makes an angle of 60° with the vertical (a) Find the tension in the string in equilibrium. (b) Suppose the ball is slightly pushed aside and released. Find the time period of the small oscillations.
A uniform electric field of 10 N C−1 exists in the vertically downward direction. Find the increase in the electric potential as one goes up through a height of 50 cm.
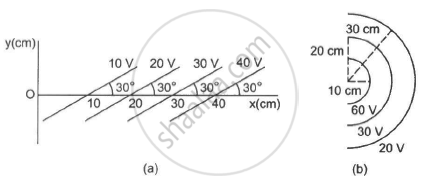
Some equipotential surface is shown in the figure. What can you say about the magnitude and the direction of the electric field?
Consider a circular ring of radius r, uniformly charged with linear charge density λ. Find the electric potential at a point on the axis at a distance x from the centre of the ring. Using this expression for the potential, find the electric field at this point.
A simple pendulum consists of a small sphere of mass m suspended by a thread of length l. The sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically downwards. Find the period of oscillation of the pendulum due to the electrostatic force acting on the sphere, neglecting the effect of the gravitational force.
The force per unit charge is known as ______.
