Advertisements
Advertisements
प्रश्न
(i) If two similar large plates, each of area A having surface charge densities +σ and –σ are separated by a distance d in air, find the expressions for
(a) field at points between the two plates and on outer side of the plates. Specify the direction of the field in each case.
(b) the potential difference between the plates.
(c) the capacitance of the capacitor so formed.
(ii) Two metallic spheres of Radii R and 2R are charged so that both of these have same surface charge density σ. If they are connected to each other with a conducting wire, inn which direction will the charge flow and why?
उत्तर
(a)
We are given two similar large plates separated by a small distance (d) and having area (A).
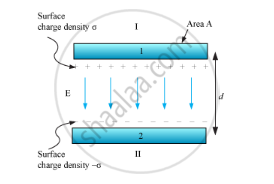
Surface charge density of plate 1, σ = Q/A, and that of plate 2 is − σ.
Electric field in different regions:
Outer region I,
`E=sigma/(2epsilon_0)-sigma/(2epsilon_0)=0`
Outer region II,
`E=sigma/(2epsilon_0)-sigma/(2epsilon_0)=0`
In the inner region between plates 1 and 2, the electric fields due to the two charged plates add up. So,
`E=sigma/(2epsilon_0)+sigma/(2epsilon_0)=sigma/epsilon_0=Q/(epsilon_0A)`
The direction of electric field is from the positive to the negative plate.
(b)
For uniform electric field, potential difference is simply the electric field multiplied by the distance between the plates, i.e.
`V=Ed=1/epsilon_0 (Qd)/A`
(c)
Capacitance C of the parallel plate capacitor,
`C=Q/V=(epsilon_0A)/d`
(ii)
We know that the potential of the metallic sphere is given by,
`V=Q/(4piepsilon_0r) `
Now, the potential of the metallic sphere of radius R is given by,
`V_R=Q/(4piepsilon_0R)`
`V_R=(sigma(4piR^2))/(4piepsilon_0R)`
`V_R=(sigmaR)/epsilon_0`
Similarly, the potential of the metallic sphere of radius 2R is given b
`V_(2R)=Q/(4piepsilon_0 2R)`
`V_(2R)=(sigma(4pi(2R)^2))/(4piepsilon_0 2R)`
`V_(2R)=(sigma2R)/epsilon_0`
from the relation (i) and (ii) we know that V2R > VR
So, when both the spheres are connected the charge flow from the sphere of radius of 2R to R.
APPEARS IN
संबंधित प्रश्न
The electric field in a region is given by `vec"E" = ("E"_0 "x")/"l" vec"i".`
Find the charge contained inside the cubical volume bound by the surfaces
x =0, x =a, y=0, y=a, z=0 and z=a. Take
`"E"_0 = 5 xx 10^3 "N""C"^-1 , "l" =2 "cm" " and" " a" = 1 "cm" `
The radius of a gold nucleus (Z = 79) is about 7.0 × 10-10 m. Assume that the positive charge is distributed uniformly throughout the nuclear volume. Find the strength of the electric field at (a) the surface of the nucleus and (b) at the middle point of a radius. Remembering that gold is a conductor, is it justified to assume that the positive charge is uniformly distributed over the entire volume of the nucleus and does not come to the outer surface?
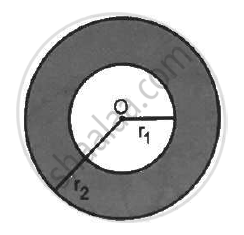
A charge Q is distributed uniformly within the material of a hollow sphere of inner and outer radii r1 and r2 (see the figure). Find the electric field at a point P at a distance x away from the centre for r1 < x < r. Draw a rough graph showing the electric field as a function of x for 0 < x < 2r2 (see the figure).
Find the magnitude of the electric field at a point 4 cm away from a line charge of density 2 × 10-6 Cm-1.
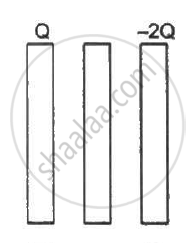
Three identical metal plates with large surface areas are kept parallel to each other as shown in the following figure. The leftmost plate is given a charge Q, the rightmost a charge −2Q and the middle one is kept neutral. Find the charge appearing on the outer surface of the rightmost plate.
A uniform field of 2.0 NC−1 exists in space in the x-direction. (a) Taking the potential at the origin to be zero, write an expression for the potential at a general point (x, y, z). (b) At which point, the potential is 25 V? (c) If the potential at the origin is taken to be 100 V, what will be the expression for the potential at a general point? (d) What will be the potential at the origin if the potential at infinity is taken to be zero? Is it practical to choose the potential at infinity to be zero?
Answer the following question.
Prove that the average energy density of the oscillating electric field is equal to that of the oscillating magnetic field.
A simple pendulum consists of a small sphere of mass m suspended by a thread of length l. The sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically downwards. Find the period of oscillation of the pendulum due to the electrostatic force acting on the sphere, neglecting the effect of the gravitational force.
A charge Q is applied to a conducting sphere of radius R. At the sphere's centre, the electric potential and electric field are respectively
Pick out the statement which is incorrect
