Advertisements
Advertisements
प्रश्न
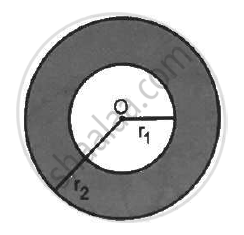
A charge Q is distributed uniformly within the material of a hollow sphere of inner and outer radii r1 and r2 (see the figure). Find the electric field at a point P at a distance x away from the centre for r1 < x < r. Draw a rough graph showing the electric field as a function of x for 0 < x < 2r2 (see the figure).
उत्तर
Amount of charge present on the hollow sphere = Q
Inner radii of the hollow sphere = r1
Outer radii of the hollow sphere = r2
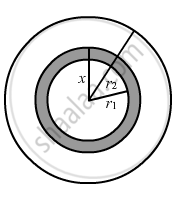
Consider an imaginary sphere of radius x.
The charge on the sphere can be found by multiplying the volume charge density of the hollow spherical volume with the volume of the imaginary sphere of radius (x-r1).
Charge per unit volume of the hollow sphere,
`ρ = "Q"/( 4/3pi("r"_2^3 -"r"_1^3))`
Charge enclosed by this imaginary sphere of radius x:-
q = ρ × Volume of the part consisting of charge
`"q" = (4/3 pi ("x"^3 -"r"_1^3)"Q")/(4/3pi ("r"_2^3))`
`"q" = (("x"^3 -"r"_1^3))/(("r"_2^3 - "r"_1^3)) "Q"`
According to Gauss's Law,
`oint "E" . "d""s" = "q"/∈_0`
Here, the surface integral is carried out on the sphere of radius x and q is the charge enclosed by this sphere.
`"E" oint "d""s" = "q"/∈_0`
`"E" (4 pi "x"^2) = "q"/∈_0`
` "E" (4 pi "x"^2) = (("x"^3 -"r"_1^3)"Q")/((("r"_2^3 -"r"_1^3)) ∈_0)`
`"E" =("Q"("x"^3 - "r"_1^3))/( 4pi ∈_0 "x"^2 ("r"_2^3 - "r"_1^3)) `
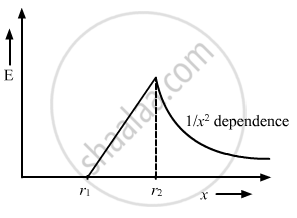
The electric field is directly proportional to x for r1 < x < r.
The electric field for r2 < x < 2r2,
`"E" = "Q" / (4 pi ∈_0 "x"^2) `
Thus, the graph can be drawn as:-
APPEARS IN
संबंधित प्रश्न
plot a graph showing the variation of current density (j) versus the electric field (E) for two conductors of different materials. What information from this plot regarding the properties of the conducting material, can be obtained which can be used to select suitable materials for use in making (i) standard resistance and (ii) connecting wires in electric circuits?
Two identical circular loops 1 and 2 of radius R each have linear charge densities −λ and +λ C/m respectively. The loops are placed coaxially with their centres `Rsqrt3` distance apart. Find the magnitude and direction of the net electric field at the centre of loop 1.
Plot a graph showing the variation of resistivity of a conductor with temperature.
A metallic particle with no net charge is placed near a finite metal plate carrying a positive charge. The electric force on the particle will be
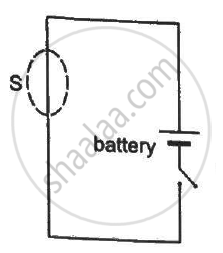
A closed surface S is constructed around a conducting wire connected to a battery and a switch in the following figure. As the switch is closed, the free electrons in the wire start moving along the wire. In any time interval, the number of electrons entering the closed surface S is equal to the number of electrons leaving it. On closing the switch, the flux of the electric field through the closed surface
(a) is increased
(b) is decreased
(c) remains unchanged
(d) remains zero
Consider the following very rough model of a beryllium atom. The nucleus has four protons and four neutrons confined to a small volume of radius 10−15 m. The two 1 selectrons make a spherical charge cloud at an average distance of 1⋅3 ×10−11 m from the nucleus, whereas the two 2 s electrons make another spherical cloud at an average distance of 5⋅2 × 10−11 m from the nucleus. Find three electric fields at (a) a point just inside the 1 s cloud and (b) a point just inside the 2 s cloud.
Find the magnitude of the electric field at a point 4 cm away from a line charge of density 2 × 10-6 Cm-1.
A long cylindrical wire carries a positive charge of linear density 2.0 × 10-8 C m -1 An electron revolves around it in a circular path under the influence of the attractive electrostatic force. Find the kinetic energy of the electron. Note that it is independent of the radius.
A non-conducting sheet of large surface area and thickness d contains a uniform charge distribution of density ρ. Find the electric field at a point P inside the plate, at a distance x from the central plane. Draw a qualitative graph of E against x for 0 < x < d.
One end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and a charge of 4.0× 10-6 C. In equilibrium, the thread makes an angle of 60° with the vertical (a) Find the tension in the string in equilibrium. (b) Suppose the ball is slightly pushed aside and released. Find the time period of the small oscillations.
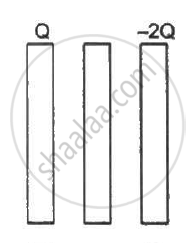
Three identical metal plates with large surface areas are kept parallel to each other as shown in the following figure. The leftmost plate is given a charge Q, the rightmost a charge −2Q and the middle one is kept neutral. Find the charge appearing on the outer surface of the rightmost plate.
Consider a circular ring of radius r, uniformly charged with linear charge density λ. Find the electric potential at a point on the axis at a distance x from the centre of the ring. Using this expression for the potential, find the electric field at this point.
Draw equipotential surfaces corresponding to a uniform electric field in the z-directions.
A simple pendulum consists of a small sphere of mass m suspended by a thread of length l. The sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically downwards. Find the period of oscillation of the pendulum due to the electrostatic force acting on the sphere, neglecting the effect of the gravitational force.
When a comb rubbed with dry hair attracts pieces of paper. This is because the ______.
The force per unit charge is known as ______.
