Advertisements
Advertisements
प्रश्न
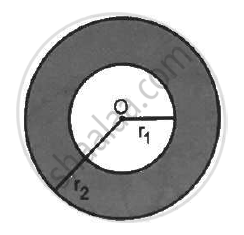
A charge Q is distributed uniformly within the material of a hollow sphere of inner and outer radii r1 and r2 (see the figure). Find the electric field at a point P at a distance x away from the centre for r1 < x < r. Draw a rough graph showing the electric field as a function of x for 0 < x < 2r2 (see the figure).
उत्तर
Amount of charge present on the hollow sphere = Q
Inner radii of the hollow sphere = r1
Outer radii of the hollow sphere = r2
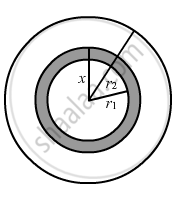
Consider an imaginary sphere of radius x.
The charge on the sphere can be found by multiplying the volume charge density of the hollow spherical volume with the volume of the imaginary sphere of radius (x-r1).
Charge per unit volume of the hollow sphere,
`ρ = "Q"/( 4/3pi("r"_2^3 -"r"_1^3))`
Charge enclosed by this imaginary sphere of radius x:-
q = ρ × Volume of the part consisting of charge
`"q" = (4/3 pi ("x"^3 -"r"_1^3)"Q")/(4/3pi ("r"_2^3))`
`"q" = (("x"^3 -"r"_1^3))/(("r"_2^3 - "r"_1^3)) "Q"`
According to Gauss's Law,
`oint "E" . "d""s" = "q"/∈_0`
Here, the surface integral is carried out on the sphere of radius x and q is the charge enclosed by this sphere.
`"E" oint "d""s" = "q"/∈_0`
`"E" (4 pi "x"^2) = "q"/∈_0`
` "E" (4 pi "x"^2) = (("x"^3 -"r"_1^3)"Q")/((("r"_2^3 -"r"_1^3)) ∈_0)`
`"E" =("Q"("x"^3 - "r"_1^3))/( 4pi ∈_0 "x"^2 ("r"_2^3 - "r"_1^3)) `
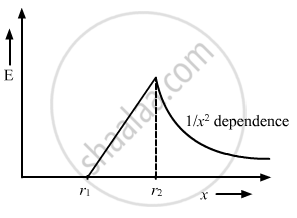
The electric field is directly proportional to x for r1 < x < r.
The electric field for r2 < x < 2r2,
`"E" = "Q" / (4 pi ∈_0 "x"^2) `
Thus, the graph can be drawn as:-
APPEARS IN
संबंधित प्रश्न
Why is the potential inside a hollow spherical charged conductor constant and has the same value of as on its surface?
A metallic particle with no net charge is placed near a finite metal plate carrying a positive charge. The electric force on the particle will be
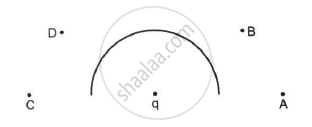
In the following figure shows a charge q placed at the centre of a hemisphere. A second charge Q is placed at one of the positions A, B, C and D. In which position(s) of this second charge, the flux of the electric field through the hemisphere remains unchanged?
(a) A
(b) B
(c) C
(d) D
A charge Q is uniformly distributed over a rod of length l. Consider a hypothetical cube of edge l with the centre of the cube at one end of the rod. Find the minimum possible flux of the electric field through the entire surface of the cube.
The electric field in a region is given by `vec"E" = ("E"_0 "x")/"l" vec"i".`
Find the charge contained inside the cubical volume bound by the surfaces
x =0, x =a, y=0, y=a, z=0 and z=a. Take
`"E"_0 = 5 xx 10^3 "N""C"^-1 , "l" =2 "cm" " and" " a" = 1 "cm" `
The radius of a gold nucleus (Z = 79) is about 7.0 × 10-10 m. Assume that the positive charge is distributed uniformly throughout the nuclear volume. Find the strength of the electric field at (a) the surface of the nucleus and (b) at the middle point of a radius. Remembering that gold is a conductor, is it justified to assume that the positive charge is uniformly distributed over the entire volume of the nucleus and does not come to the outer surface?
A long cylindrical wire carries a positive charge of linear density 2.0 × 10-8 C m -1 An electron revolves around it in a circular path under the influence of the attractive electrostatic force. Find the kinetic energy of the electron. Note that it is independent of the radius.
A charged particle with a charge of −2⋅0 × 10−6 C is placed close to a non-conducting plate with a surface charge density of 4.0 × 10-6Cm0-2. Find the force of attraction between the particle and the plate.
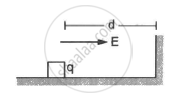
A block of mass containing a net positive charge q is placed on a smooth horizontal table which terminates in a vertical wall as shown in the figure. The distance of the block from the wall is d. A horizontal electric field E towards the right is switched on. Assuming elastic collisions (if any), find the time period of the resulting oscillatory motion. Is it a simple harmonic motion?
Consider a circular ring of radius r, uniformly charged with linear charge density λ. Find the electric potential at a point on the axis at a distance x from the centre of the ring. Using this expression for the potential, find the electric field at this point.
Draw equipotential surfaces corresponding to a uniform electric field in the z-directions.
Answer the following question.
Prove that the average energy density of the oscillating electric field is equal to that of the oscillating magnetic field.
The force per unit charge is known as ______.
Two charged conducting spheres of radii a and b are connected to each other by a wire. Find the ratio of the electric fields at their surfaces.
