Advertisements
Advertisements
Question
(i) If two similar large plates, each of area A having surface charge densities +σ and –σ are separated by a distance d in air, find the expressions for
(a) field at points between the two plates and on outer side of the plates. Specify the direction of the field in each case.
(b) the potential difference between the plates.
(c) the capacitance of the capacitor so formed.
(ii) Two metallic spheres of Radii R and 2R are charged so that both of these have same surface charge density σ. If they are connected to each other with a conducting wire, inn which direction will the charge flow and why?
Solution
(a)
We are given two similar large plates separated by a small distance (d) and having area (A).
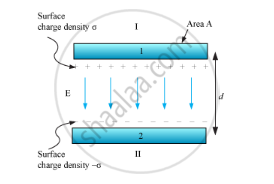
Surface charge density of plate 1, σ = Q/A, and that of plate 2 is − σ.
Electric field in different regions:
Outer region I,
`E=sigma/(2epsilon_0)-sigma/(2epsilon_0)=0`
Outer region II,
`E=sigma/(2epsilon_0)-sigma/(2epsilon_0)=0`
In the inner region between plates 1 and 2, the electric fields due to the two charged plates add up. So,
`E=sigma/(2epsilon_0)+sigma/(2epsilon_0)=sigma/epsilon_0=Q/(epsilon_0A)`
The direction of electric field is from the positive to the negative plate.
(b)
For uniform electric field, potential difference is simply the electric field multiplied by the distance between the plates, i.e.
`V=Ed=1/epsilon_0 (Qd)/A`
(c)
Capacitance C of the parallel plate capacitor,
`C=Q/V=(epsilon_0A)/d`
(ii)
We know that the potential of the metallic sphere is given by,
`V=Q/(4piepsilon_0r) `
Now, the potential of the metallic sphere of radius R is given by,
`V_R=Q/(4piepsilon_0R)`
`V_R=(sigma(4piR^2))/(4piepsilon_0R)`
`V_R=(sigmaR)/epsilon_0`
Similarly, the potential of the metallic sphere of radius 2R is given b
`V_(2R)=Q/(4piepsilon_0 2R)`
`V_(2R)=(sigma(4pi(2R)^2))/(4piepsilon_0 2R)`
`V_(2R)=(sigma2R)/epsilon_0`
from the relation (i) and (ii) we know that V2R > VR
So, when both the spheres are connected the charge flow from the sphere of radius of 2R to R.
APPEARS IN
RELATED QUESTIONS
plot a graph showing the variation of current density (j) versus the electric field (E) for two conductors of different materials. What information from this plot regarding the properties of the conducting material, can be obtained which can be used to select suitable materials for use in making (i) standard resistance and (ii) connecting wires in electric circuits?
A metallic particle with no net charge is placed near a finite metal plate carrying a positive charge. The electric force on the particle will be
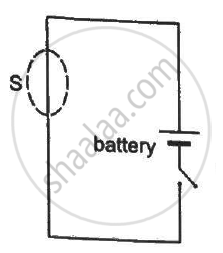
A closed surface S is constructed around a conducting wire connected to a battery and a switch in the following figure. As the switch is closed, the free electrons in the wire start moving along the wire. In any time interval, the number of electrons entering the closed surface S is equal to the number of electrons leaving it. On closing the switch, the flux of the electric field through the closed surface
(a) is increased
(b) is decreased
(c) remains unchanged
(d) remains zero
A charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius a. (a) Find the surface. (b) If a charge q is put on the sphere, what would be the surface charge densities on the inner and outer surfaces? (c) Find the electric field inside the sphere at a distance x from the centre in the situations (a) and (b).
A charged particle with a charge of −2⋅0 × 10−6 C is placed close to a non-conducting plate with a surface charge density of 4.0 × 10-6Cm0-2. Find the force of attraction between the particle and the plate.
One end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and a charge of 4.0× 10-6 C. In equilibrium, the thread makes an angle of 60° with the vertical (a) Find the tension in the string in equilibrium. (b) Suppose the ball is slightly pushed aside and released. Find the time period of the small oscillations.
A uniform electric field of 10 N C−1 exists in the vertically downward direction. Find the increase in the electric potential as one goes up through a height of 50 cm.
A uniform field of 2.0 NC−1 exists in space in the x-direction. (a) Taking the potential at the origin to be zero, write an expression for the potential at a general point (x, y, z). (b) At which point, the potential is 25 V? (c) If the potential at the origin is taken to be 100 V, what will be the expression for the potential at a general point? (d) What will be the potential at the origin if the potential at infinity is taken to be zero? Is it practical to choose the potential at infinity to be zero?
Answer the following question.
Prove that the average energy density of the oscillating electric field is equal to that of the oscillating magnetic field.
