Advertisements
Advertisements
Question
plot a graph showing the variation of current density (j) versus the electric field (E) for two conductors of different materials. What information from this plot regarding the properties of the conducting material, can be obtained which can be used to select suitable materials for use in making (i) standard resistance and (ii) connecting wires in electric circuits?
Solution
The current density j is related to electric field as
E = σ E
Here, σ is the conductivity of the material.
The above relation is equivalent to Ohm’s law.
Now, for a given material, σ is a constant.
Hence, the plot of j versus E will be a straight line starting from the origin.
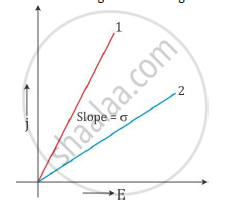
The slope of the graph gives the conductivity σ of the material.
The graph with a greater slope is a better conductor and the graph with a lesser slope is a poor conductor than the other.
(i) To make a standard resistance: A resistor should allow only a limited current to flow through it. Hence, from the graph, we come to know that the material whose plot is similar to plot (2) should be used to make a resistor.
(ii) To make a connecting wire: A wire should allow all the current to flow through it without resisting it. So, it should have a higher conductivity. Hence, from the graph, we come to know that the material whose plot is similar to plot (1) should be used to make a wire.
APPEARS IN
RELATED QUESTIONS
(i) If two similar large plates, each of area A having surface charge densities +σ and –σ are separated by a distance d in air, find the expressions for
(a) field at points between the two plates and on outer side of the plates. Specify the direction of the field in each case.
(b) the potential difference between the plates.
(c) the capacitance of the capacitor so formed.
(ii) Two metallic spheres of Radii R and 2R are charged so that both of these have same surface charge density σ. If they are connected to each other with a conducting wire, inn which direction will the charge flow and why?
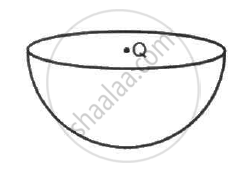
A charge Q is placed at the centre of an imaginary hemispherical surface. Using symmetry arguments and Gauss's Law, find the flux of the electric field due to this charge through the surface of the hemisphere in the following figure.
A long cylindrical wire carries a positive charge of linear density 2.0 × 10-8 C m -1 An electron revolves around it in a circular path under the influence of the attractive electrostatic force. Find the kinetic energy of the electron. Note that it is independent of the radius.
A charged particle with a charge of −2⋅0 × 10−6 C is placed close to a non-conducting plate with a surface charge density of 4.0 × 10-6Cm0-2. Find the force of attraction between the particle and the plate.
A simple pendulum consists of a small sphere of mass m suspended by a thread of length l. The sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically downwards. Find the period of oscillation of the pendulum due to the electrostatic force acting on the sphere, neglecting the effect of the gravitational force.
Two charged conducting spheres of radii a and b are connected to each other by a wire. Find the ratio of the electric fields at their surfaces.
