Advertisements
Advertisements
Question
A long cylindrical wire carries a positive charge of linear density 2.0 × 10-8 C m -1 An electron revolves around it in a circular path under the influence of the attractive electrostatic force. Find the kinetic energy of the electron. Note that it is independent of the radius.
Solution
Let the linear charge density of the wire be λ.
The electric field due to a charge distributed on a wire at a perpendicular distance rfrom the wire,
`"E" = λ/ (2 pi ∈ _0 "r")`
The electrostatic force on the electron will provide the electron the necessary centripetal force required by it to move in a circular orbit. Thus,
`"qE" = ("m""v"^2)/"r"`
⇒ mv2 = qEr .. (1)
Kinetic energy of the electron,`"K" = 1/2 mv2`
From (1),
`"K" = ("qEr")/2`
`"K" = "qr"/2 λ /(2 pi ∈_0 "r")` `[∵ "E" = λ/((2 pi ∈_0 "r")) ]`
K =(1.6 ×10-19) × ( 2 × 10-8) × ( 9 × 109)J
K = 2.88 × 10-17 J
APPEARS IN
RELATED QUESTIONS
(i) If two similar large plates, each of area A having surface charge densities +σ and –σ are separated by a distance d in air, find the expressions for
(a) field at points between the two plates and on outer side of the plates. Specify the direction of the field in each case.
(b) the potential difference between the plates.
(c) the capacitance of the capacitor so formed.
(ii) Two metallic spheres of Radii R and 2R are charged so that both of these have same surface charge density σ. If they are connected to each other with a conducting wire, inn which direction will the charge flow and why?
Plot a graph showing the variation of resistivity of a conductor with temperature.
A charge Q is uniformly distributed over a large plastic plate. The electric field at a point P close to the centre of the plate is 10 V m−1. If the plastic plate is replaced by a copper plate of the same geometrical dimensions and carrying the same charge Q, the electric field at the point P will become
A metallic particle with no net charge is placed near a finite metal plate carrying a positive charge. The electric force on the particle will be
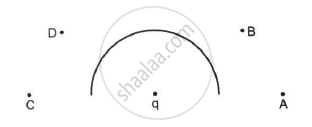
In the following figure shows a charge q placed at the centre of a hemisphere. A second charge Q is placed at one of the positions A, B, C and D. In which position(s) of this second charge, the flux of the electric field through the hemisphere remains unchanged?
(a) A
(b) B
(c) C
(d) D
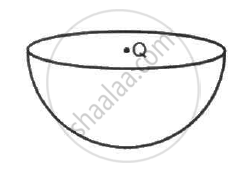
A charge Q is placed at the centre of an imaginary hemispherical surface. Using symmetry arguments and Gauss's Law, find the flux of the electric field due to this charge through the surface of the hemisphere in the following figure.
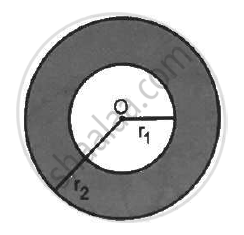
A charge Q is distributed uniformly within the material of a hollow sphere of inner and outer radii r1 and r2 (see the figure). Find the electric field at a point P at a distance x away from the centre for r1 < x < r. Draw a rough graph showing the electric field as a function of x for 0 < x < 2r2 (see the figure).
A charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius a. (a) Find the surface. (b) If a charge q is put on the sphere, what would be the surface charge densities on the inner and outer surfaces? (c) Find the electric field inside the sphere at a distance x from the centre in the situations (a) and (b).
Consider the following very rough model of a beryllium atom. The nucleus has four protons and four neutrons confined to a small volume of radius 10−15 m. The two 1 selectrons make a spherical charge cloud at an average distance of 1⋅3 ×10−11 m from the nucleus, whereas the two 2 s electrons make another spherical cloud at an average distance of 5⋅2 × 10−11 m from the nucleus. Find three electric fields at (a) a point just inside the 1 s cloud and (b) a point just inside the 2 s cloud.
A non-conducting sheet of large surface area and thickness d contains a uniform charge distribution of density ρ. Find the electric field at a point P inside the plate, at a distance x from the central plane. Draw a qualitative graph of E against x for 0 < x < d.
Some equipotential surface is shown in the figure. What can you say about the magnitude and the direction of the electric field?
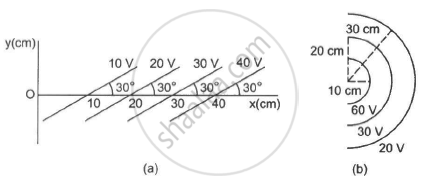
Answer the following question.
Prove that the average energy density of the oscillating electric field is equal to that of the oscillating magnetic field.
A simple pendulum consists of a small sphere of mass m suspended by a thread of length l. The sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically downwards. Find the period of oscillation of the pendulum due to the electrostatic force acting on the sphere, neglecting the effect of the gravitational force.
Electric field at a point is defined as ______.
The force per unit charge is known as ______.
Pick out the statement which is incorrect
