Advertisements
Advertisements
Question
A long cylindrical volume contains a uniformly distributed charge of density ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (see the figure).
Solution
Given:-
Volume charge density inside the cylinder = ρ
Let the radius of the cylinder be r.
Let charge enclosed by the given cylinder be Q
Consider a Gaussian cylindrical surface of radius x and height h.
Let charge enclosed by the cylinder of radius x be q'.
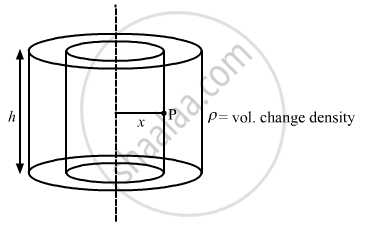
The charge on this imaginary cylinder can be found by taking the product of the volume charge density of the cylinder and the volume of the imaginary cylinder. Thus, q' = ρ( π x2 h)
From Gauss's Law,
`oint "E" . "ds" = ("q"_"en")/∈_0`
`"E" . 2 pi "xh" = (ρ( pi "x"^2 "h"))/ ∈_0`
`"E" = (ρ"x")/(2∈_0)`
APPEARS IN
RELATED QUESTIONS
A polythene piece rubbed with wool is found to have a negative charge of 3 × 10−7 C.
(a) Estimate the number of electrons transferred (from which to which?)
(b) Is there a transfer of mass from wool to polythene?
Write the expression for the displacement current in terms of the rate of change of electric flux.
A point charge q is placed in a cavity in a metal block. If a charge Q is brought outside the metal, will the charge q feel an electric fore?
Two large conducting plates are placed parallel to each other with a separation of 2⋅00 cm between them. An electron starting from rest near one of the plates reaches the other plate in 2⋅00 microseconds. Find the surface charge density on the inner surfaces.
Two particles A and B with charges q and 2q, respectively, are placed on a smooth table with a separation d. A third particle C is to be clamped on the table in such a way that the particles A and B remain at rest on the table under electrical forces. What should be the charge on C and where should it be clamped?
Two small conducting spheres of equal radius have charges +10 µC and -20 µC respectively and placed at a distance R from each other experience force F1· If they are brought in contact and separated to the same distance, they experience force F2. The ratio of F1 to F2 is ____________.
Two charges q1 and q2 are placed in vacuum at a distance d and the force acting between them is F. If a medium of dielectric constant 4 is introduced around them, the force now will be ______.
A positive charge particle of 100 mg is thrown in opposite direction to a uniform electric field of strength 1 × 105 NC–1. If the charge on the particle is 40 μC and the initial velocity is 200 ms-1, how much distance it will travel before coming to the rest momentarily ______.
A charge of 4 µC is to be divided into two. The distance between the two divided charges is constant. The magnitude of the divided charges so that the force between them is maximum, will be:
Two identical conducting spheres with negligible volume have 2.1 nC and -0.1 nC charges, respectively. They are brought into contact and then separated by a distance of 0.5 m. The electrostatic force acting between the spheres is ______ × 10-9N.
[Given: 4πε0 = `1/(9xx10^9)` SI unit]
Two identical conducting spheres A and B, carry equal charge. They are separated by a distance much larger than their diameter, and the force between them is F. A third identical conducting sphere, C, is uncharged. Sphere C is first touched to A, then to B, and then removed. As a result, the force between A and B would be equal to ______.
A straight infinitely long cylinder of radius R0 = 10 cm is uniformly charged with a surface charge density σ = + 10-12 C/m2. The cylinder serves as a source of electrons, with the velocity of the emitted electrons perpendicular to its surface. Electron velocity must be ______ × 105 m/s to ensure that electrons can move away, from the axis of the cylinder to a distance greater than r = 103 m.
The electrostatic potential inside a charged spherical ball is given by `Phi = ar^2 + b`, where r is the distance from the centre a, and b are constants. Then the charge density inside the ball is ______.
The potential at a point x (measured in µm) due to some charges situated on the X-axis is given by v(x) = `20/((x^2 - 4)` V. The electric field E at x = 4 µm is given by ______.
