Advertisements
Advertisements
Question
Two large conducting plates are placed parallel to each other with a separation of 2⋅00 cm between them. An electron starting from rest near one of the plates reaches the other plate in 2⋅00 microseconds. Find the surface charge density on the inner surfaces.
Solution
Distance travelled by the electron, d= 2 cm
Time taken to cross the region, t = 2× 10-6 s
Let the surface charge density at the conducting plates be σ.
Let the acceleration of the electron be a.
Applying the 2nd equation of motion, we get:
`"d" = 1/2 "a""t"^2`
`=> "a" = (2"d")/"t"^2`
This acceleration is provided by the Coulombic force. So,
`"a" = "qE"/m = "2d"/"t"^2`
`=> "E" = (2"md")/"qt"^2`
`"E" = (2 xx (9.1xx10^-31) xx (2 xx 10^-2))/((1.6 xx 10^-19) xx ( 4 xx 10^-12)`
E = 5.6875 × 10-2 N/C
Also, we know that electric field due to a plate,
`"E" = sigma/∈_0`
⇒ σ =∈_0 E
⇒ σ = ( 8.85 × 10-12) × ( 5.68 × 10-2 ) C/m2
⇒ σ = 50.33 × 10-14 C/m2 = 0.503 × 10-12 C/m2
APPEARS IN
RELATED QUESTIONS
A polythene piece rubbed with wool is found to have a negative charge of 3 × 10−7 C.
(a) Estimate the number of electrons transferred (from which to which?)
(b) Is there a transfer of mass from wool to polythene?
How does Ampere-Maxwell law explain the flow of current through a capacitor when it is being charged by a battery?
Write the expression for the displacement current in terms of the rate of change of electric flux.
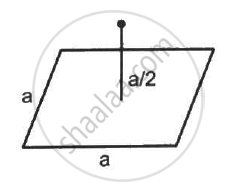
A charge Q is placed at a distance a/2 above the centre of a horizontal, square surface of edge a as shown in the following figure . Find the flux of the electric field through the square surface.
Two particles A and B, each with a charge Q, are placed a distance d apart. Where should a particle of charge q be placed on the perpendicular bisector of AB, so that it experiences maximum force? What is the magnitude of this maximum force?
The electric force experienced by a charge of 1.0 × 10−6 C is 1.5 × 10−3 N. Find the magnitude of the electric field at the position of the charge.
A positive charge q is placed in front of a conducting solid cube at a distance d from its centre. Find the electric field at the centre of the cube to the charges appearing on its surface.
One metallic sphere A is given a positive charge whereas another identical metallic sphere B of exactly the same mass as A is given an equal amount of negative charge. Then
A conducting sphere of radius 0.104 m has an unknown charge. If the electric field at 0.20 m from the centre of the sphere is 1.5 x 103 NC-1 and points radially inward, what is the electric flux?
Assertion: The positive charge particle is placed in front of a spherical uncharged conductor. The number of lines of forces terminating on the sphere will be more than those emerging from it.
Reason: The surface charge density at a point on the sphere nearest to the point charge will be negative and maximum in magnitude compared to other points on the sphere.
Electric field lines provide information about ______.
Which one of the following is the unit of electric charge?
A metallic spherical shell has an inner radius R1 and outer radius R2. A charge Q is placed at the centre of the spherical cavity. What will be surface charge density on (i) the inner surface, and (ii) the outer surface?
Two identical metallic spheres A and B when placed at certain distance in air repel each other with a force of F. Another identical uncharged sphere C is first placed in contact with A and then in contact with B and finally placed at midpoint between spheres A and B. The force experienced by sphere C will be:
A particle of mass m and charge q is placed at rest in a uniform electric field E and then released. The kinetic energy gained by the particle after moving a distance of y will be ______.
The potential at a point x (measured in µm) due to some charges situated on the X-axis is given by v(x) = `20/((x^2 - 4)` V. The electric field E at x = 4 µm is given by ______.
