Advertisements
Advertisements
Question
Two particles A and B, each with a charge Q, are placed a distance d apart. Where should a particle of charge q be placed on the perpendicular bisector of AB, so that it experiences maximum force? What is the magnitude of this maximum force?
Solution
Let the charge q be placed at a distance x on the perpendicular bisector of AB.
As shown in the figure, the horizontal component of force is balanced.
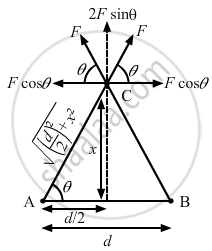
\[\sin\theta = \frac{x}{\sqrt{\left( \frac{d}{2} \right)^2 + x^2}}\]
Total vertical component of force,
\[F' = 2F\sin\theta\]
\[F' = 2 \times \frac{1}{4\pi \epsilon_0} \times \frac{qQ}{\left( \frac{d}{2} \right)^2 + x^2} \times \frac{x}{\sqrt{\left( \frac{d}{2} \right)^2 + x^2}}\]
\[ \Rightarrow F' = \frac{1}{2\pi \epsilon_0} \times \frac{qQx}{\left[ \left( \frac{d}{2} \right)^2 + x^2 \right]^{3/2}}\]
For maximum force, \[\frac{dF'}{dx} = 0\]
\[\frac{qQ}{2\pi \epsilon_0} \times \left[ \left[ \left( \frac{d}{2} \right)^2 + x^2 \right]^{- 3/2} - x\frac{3}{2} \left[ \left( \frac{d}{2} \right)^2 + x^2 \right]^{- 5/2} 2x \right] = 0\]
\[ \Rightarrow \left( \frac{d}{2} \right)^2 + x^2 - 3 x^2 = 0\]
\[ \Rightarrow 2 x^2 = \left( \frac{d}{2} \right)^2 \]
\[ \Rightarrow x = \frac{d}{2\sqrt{2}}\]
\[ \therefore F '_\max = \frac{1}{2\pi \epsilon_0}\frac{qQ\frac{d}{2\sqrt{2}}}{\left[ \left( \frac{d}{2} \right)^2 + \left( \frac{d}{2\sqrt{2}} \right)^2 \right]^{3/2}}\]
\[ = 3 . 08\frac{Qq}{4\pi \epsilon_0 d^2}\]
APPEARS IN
RELATED QUESTIONS
A conducting sphere of radius 10 cm has an unknown charge. If the electric field 20 cm from the centre of the sphere is 1.5 × 103 N/C and points radially inward, what is the net charge on the sphere?
How does Ampere-Maxwell law explain the flow of current through a capacitor when it is being charged by a battery?
A point charge is brought inside an electric field. The electric field at a nearby point
(a) will increase if the charge is positive
(b) will decrease if the charge is negative
(c) may increase if the charge is positive
(d) may decrease if the charge is negative
Two particles A and B with charges q and 2q, respectively, are placed on a smooth table with a separation d. A third particle C is to be clamped on the table in such a way that the particles A and B remain at rest on the table under electrical forces. What should be the charge on C and where should it be clamped?
A rod of length L has a total charge Q distributed uniformly along its length. It is bent in the shape of a semicircle. Find the magnitude of the electric field at the centre of curvature of the semicircle.
Choose the correct option.
Two point charges of +5 μC are so placed that they experience a force of 8.0 × 10-3N. They are then moved apart so that the force is now 2.0 × 10-3N. The distance between them is now
Answer the following question.
What is the magnitude of the charge on an electron?
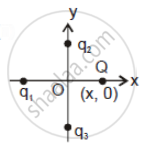
In figure two positive charges q2 and q3 fixed along the y-axis, exert a net electric force in the + x-direction on a charge q1 fixed along the x-axis. If a positive charge Q is added at (x, 0), the force on q1 ______.
(1) |
(2) |
Electric field lines provide information about ______.
When a glass rod is rubbed with silk, it ______.
Two charges q1 and q2 are placed in vacuum at a distance d and the force acting between them is F. If a medium of dielectric constant 4 is introduced around them, the force now will be ______.
Total charge –Q is uniformly spread along length of a ring of radius R. A small test charge +q of mass m is kept at the centre of the ring and is given a gentle push along the axis of the ring.
- Show that the particle executes a simple harmonic oscillation.
- Obtain its time period.
Given below are two statements:
- Statement I: The electric force changes the speed of the charged particle and hence changes its kinetic energy; whereas the magnetic force does not change the kinetic energy of the charged particle.
- Statement II: The electric force accelerates the positively charged particle perpendicular to the direction of the electric field. The magnetic force accelerates the moving charged particle along the direction of the magnetic field.
In light of the above statements, choose the most appropriate answer from the options given below.
A charge of 4 µC is to be divided into two. The distance between the two divided charges is constant. The magnitude of the divided charges so that the force between them is maximum, will be:
Two identical conducting spheres with negligible volume have 2.1 nC and -0.1 nC charges, respectively. They are brought into contact and then separated by a distance of 0.5 m. The electrostatic force acting between the spheres is ______ × 10-9N.
[Given: 4πε0 = `1/(9xx10^9)` SI unit]
Two identical conducting spheres A and B, carry equal charge. They are separated by a distance much larger than their diameter, and the force between them is F. A third identical conducting sphere, C, is uncharged. Sphere C is first touched to A, then to B, and then removed. As a result, the force between A and B would be equal to ______.
