Advertisements
Advertisements
प्रश्न
plot a graph showing the variation of current density (j) versus the electric field (E) for two conductors of different materials. What information from this plot regarding the properties of the conducting material, can be obtained which can be used to select suitable materials for use in making (i) standard resistance and (ii) connecting wires in electric circuits?
उत्तर
The current density j is related to electric field as
E = σ E
Here, σ is the conductivity of the material.
The above relation is equivalent to Ohm’s law.
Now, for a given material, σ is a constant.
Hence, the plot of j versus E will be a straight line starting from the origin.
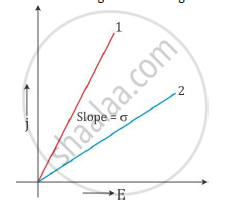
The slope of the graph gives the conductivity σ of the material.
The graph with a greater slope is a better conductor and the graph with a lesser slope is a poor conductor than the other.
(i) To make a standard resistance: A resistor should allow only a limited current to flow through it. Hence, from the graph, we come to know that the material whose plot is similar to plot (2) should be used to make a resistor.
(ii) To make a connecting wire: A wire should allow all the current to flow through it without resisting it. So, it should have a higher conductivity. Hence, from the graph, we come to know that the material whose plot is similar to plot (1) should be used to make a wire.
APPEARS IN
संबंधित प्रश्न
The electric field in a region is given by
`vec"E"= 3/5"E"_0 vec"i" + 4/5 "E"_0 vec "i" "with" " E"_0 = 2.0 xx 10^3 "N""C"^-1.`
Find the flux of this field through a rectangular surface of area 0⋅2 m2 parallel to the y-z plane.
The electric field in a region is given by `vec"E" = ("E"_0 "x")/"l" vec"i".`
Find the charge contained inside the cubical volume bound by the surfaces
x =0, x =a, y=0, y=a, z=0 and z=a. Take
`"E"_0 = 5 xx 10^3 "N""C"^-1 , "l" =2 "cm" " and" " a" = 1 "cm" `
A charged particle with a charge of −2⋅0 × 10−6 C is placed close to a non-conducting plate with a surface charge density of 4.0 × 10-6Cm0-2. Find the force of attraction between the particle and the plate.
One end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and a charge of 4.0× 10-6 C. In equilibrium, the thread makes an angle of 60° with the vertical (a) Find the tension in the string in equilibrium. (b) Suppose the ball is slightly pushed aside and released. Find the time period of the small oscillations.
A uniform field of 2.0 NC−1 exists in space in the x-direction. (a) Taking the potential at the origin to be zero, write an expression for the potential at a general point (x, y, z). (b) At which point, the potential is 25 V? (c) If the potential at the origin is taken to be 100 V, what will be the expression for the potential at a general point? (d) What will be the potential at the origin if the potential at infinity is taken to be zero? Is it practical to choose the potential at infinity to be zero?
Answer the following question.
Prove that the average energy density of the oscillating electric field is equal to that of the oscillating magnetic field.
A charge Q is applied to a conducting sphere of radius R. At the sphere's centre, the electric potential and electric field are respectively
Two charged conducting spheres of radii a and b are connected to each other by a wire. Find the ratio of the electric fields at their surfaces.
