Advertisements
Advertisements
Question
A uniform electric field of 10 N C−1 exists in the vertically downward direction. Find the increase in the electric potential as one goes up through a height of 50 cm.
Solution
Electric field intensity, E = 10 N/C,
Change in height, ds = 50 cm = `1/2`m
Change in electric potential, dV = E.ds = 10 × `1/2= 5` V
APPEARS IN
RELATED QUESTIONS
Plot a graph showing the variation of resistivity of a conductor with temperature.
Why is the potential inside a hollow spherical charged conductor constant and has the same value of as on its surface?
A metallic particle with no net charge is placed near a finite metal plate carrying a positive charge. The electric force on the particle will be
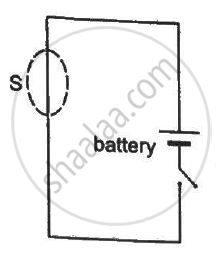
A closed surface S is constructed around a conducting wire connected to a battery and a switch in the following figure. As the switch is closed, the free electrons in the wire start moving along the wire. In any time interval, the number of electrons entering the closed surface S is equal to the number of electrons leaving it. On closing the switch, the flux of the electric field through the closed surface
(a) is increased
(b) is decreased
(c) remains unchanged
(d) remains zero
Show that there can be no net charge in a region in which the electric field is uniform at all points.
The electric field in a region is given by
`vec"E"= 3/5"E"_0 vec"i" + 4/5 "E"_0 vec "i" "with" " E"_0 = 2.0 xx 10^3 "N""C"^-1.`
Find the flux of this field through a rectangular surface of area 0⋅2 m2 parallel to the y-z plane.
The electric field in a region is given by `vec"E" = ("E"_0 "x")/"l" vec"i".`
Find the charge contained inside the cubical volume bound by the surfaces
x =0, x =a, y=0, y=a, z=0 and z=a. Take
`"E"_0 = 5 xx 10^3 "N""C"^-1 , "l" =2 "cm" " and" " a" = 1 "cm" `
The radius of a gold nucleus (Z = 79) is about 7.0 × 10-10 m. Assume that the positive charge is distributed uniformly throughout the nuclear volume. Find the strength of the electric field at (a) the surface of the nucleus and (b) at the middle point of a radius. Remembering that gold is a conductor, is it justified to assume that the positive charge is uniformly distributed over the entire volume of the nucleus and does not come to the outer surface?
Find the magnitude of the electric field at a point 4 cm away from a line charge of density 2 × 10-6 Cm-1.
A long cylindrical wire carries a positive charge of linear density 2.0 × 10-8 C m -1 An electron revolves around it in a circular path under the influence of the attractive electrostatic force. Find the kinetic energy of the electron. Note that it is independent of the radius.
A non-conducting sheet of large surface area and thickness d contains a uniform charge distribution of density ρ. Find the electric field at a point P inside the plate, at a distance x from the central plane. Draw a qualitative graph of E against x for 0 < x < d.
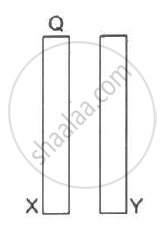
Two conducting plates X and Y, each with a large surface area A (on one side), are placed parallel to each other, as shown in the following figure . Plate X is given a charge Q,whereas the other is kept neutral. Find (a) the surface charge density at the inner surface of plate X (b) the electric field at a point to the left of the plates (c) the electric field at a point in between the plates and (d) the electric field at a point to the right of the plates.
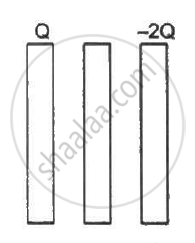
Three identical metal plates with large surface areas are kept parallel to each other as shown in the following figure. The leftmost plate is given a charge Q, the rightmost a charge −2Q and the middle one is kept neutral. Find the charge appearing on the outer surface of the rightmost plate.
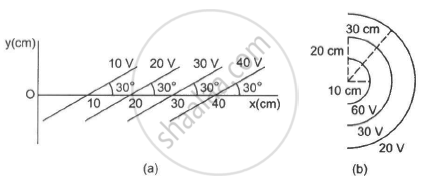
Some equipotential surface is shown in the figure. What can you say about the magnitude and the direction of the electric field?
A uniform field of 2.0 NC−1 exists in space in the x-direction. (a) Taking the potential at the origin to be zero, write an expression for the potential at a general point (x, y, z). (b) At which point, the potential is 25 V? (c) If the potential at the origin is taken to be 100 V, what will be the expression for the potential at a general point? (d) What will be the potential at the origin if the potential at infinity is taken to be zero? Is it practical to choose the potential at infinity to be zero?
Electric field at a point is defined as ______.
When a comb rubbed with dry hair attracts pieces of paper. This is because the ______.
