Advertisements
Advertisements
Question
Three identical metal plates with large surface areas are kept parallel to each other as shown in the following figure. The leftmost plate is given a charge Q, the rightmost a charge −2Q and the middle one is kept neutral. Find the charge appearing on the outer surface of the rightmost plate.
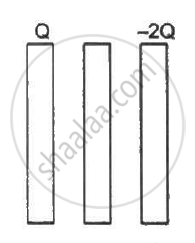
Solution

Consider the Gaussian surface as shown in the figure.
Let the charge on the outer surface of the left-most plate be q. Thus, the charges on the plates are distributed as shown in the following diagram.
The net field at point P due to all the induced charges must be zero, as it is lying inside the metal surface.
Let the surface area of the plates be A.
Electric field at point P due to the charges on plate X:-
Due to charge (+ Q -q) is `("Q" -"q")/(2"A"∈_0)` in the right direction
Due to charge (+q) is `"q"/(2"A"∈_0)` in the right direction
Electric field at point P due to charges on plate Y:-
Due to charge (-q) is `"q"/(2"A"∈_0)` in the right direction
Due to charge (+q) is `"q"/(2"A"∈_0)` in the left direction.
Electric field at point P due to charges on plate Z:-
Due to charge (-q) is `"q"/(2"A"∈_0)` in the right direction.
Due to charge (-2Q+q) is `(2"Q"-"q")/(2"A"∈_0)` in the right direction
The net electric field at point P:-
`("Q"-"q")/(2"A"∈_0)+"q"/(2"A"∈_0) -"q"/(2"A"∈_0) - "q"/(2"A"∈_0) + "q"/(2"A"∈_0) + (2"Q"-"q")/(2"A"∈_0) = 0`
`("Q"-"q")/(2"A"∈_0) + (2"Q" -"q")/(2"A"∈_0) = 0`
`Q - q + 2Q - q = 0`
`3Q - q = 0`
`"q" =(3"Q")/2`
Thus, the charge on the outer plate of the right-most plate = `-2"Q" +"q" = -2"Q"+ (3"Q")/2 = -"Q"/2`
APPEARS IN
RELATED QUESTIONS
(i) If two similar large plates, each of area A having surface charge densities +σ and –σ are separated by a distance d in air, find the expressions for
(a) field at points between the two plates and on outer side of the plates. Specify the direction of the field in each case.
(b) the potential difference between the plates.
(c) the capacitance of the capacitor so formed.
(ii) Two metallic spheres of Radii R and 2R are charged so that both of these have same surface charge density σ. If they are connected to each other with a conducting wire, inn which direction will the charge flow and why?
plot a graph showing the variation of current density (j) versus the electric field (E) for two conductors of different materials. What information from this plot regarding the properties of the conducting material, can be obtained which can be used to select suitable materials for use in making (i) standard resistance and (ii) connecting wires in electric circuits?
A charge Q is uniformly distributed over a large plastic plate. The electric field at a point P close to the centre of the plate is 10 V m−1. If the plastic plate is replaced by a copper plate of the same geometrical dimensions and carrying the same charge Q, the electric field at the point P will become
A charge Q is uniformly distributed over a rod of length l. Consider a hypothetical cube of edge l with the centre of the cube at one end of the rod. Find the minimum possible flux of the electric field through the entire surface of the cube.
The electric field in a region is given by
`vec"E"= 3/5"E"_0 vec"i" + 4/5 "E"_0 vec "i" "with" " E"_0 = 2.0 xx 10^3 "N""C"^-1.`
Find the flux of this field through a rectangular surface of area 0⋅2 m2 parallel to the y-z plane.
The electric field in a region is given by `vec"E" = ("E"_0 "x")/"l" vec"i".`
Find the charge contained inside the cubical volume bound by the surfaces
x =0, x =a, y=0, y=a, z=0 and z=a. Take
`"E"_0 = 5 xx 10^3 "N""C"^-1 , "l" =2 "cm" " and" " a" = 1 "cm" `
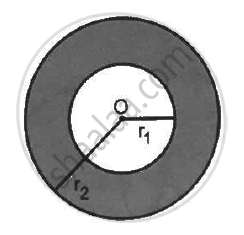
A charge Q is distributed uniformly within the material of a hollow sphere of inner and outer radii r1 and r2 (see the figure). Find the electric field at a point P at a distance x away from the centre for r1 < x < r. Draw a rough graph showing the electric field as a function of x for 0 < x < 2r2 (see the figure).
Find the magnitude of the electric field at a point 4 cm away from a line charge of density 2 × 10-6 Cm-1.
A non-conducting sheet of large surface area and thickness d contains a uniform charge distribution of density ρ. Find the electric field at a point P inside the plate, at a distance x from the central plane. Draw a qualitative graph of E against x for 0 < x < d.
One end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and a charge of 4.0× 10-6 C. In equilibrium, the thread makes an angle of 60° with the vertical (a) Find the tension in the string in equilibrium. (b) Suppose the ball is slightly pushed aside and released. Find the time period of the small oscillations.
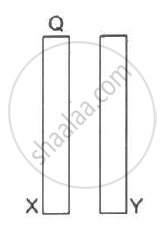
Two conducting plates X and Y, each with a large surface area A (on one side), are placed parallel to each other, as shown in the following figure . Plate X is given a charge Q,whereas the other is kept neutral. Find (a) the surface charge density at the inner surface of plate X (b) the electric field at a point to the left of the plates (c) the electric field at a point in between the plates and (d) the electric field at a point to the right of the plates.
A uniform electric field of 10 N C−1 exists in the vertically downward direction. Find the increase in the electric potential as one goes up through a height of 50 cm.
A uniform field of 2.0 NC−1 exists in space in the x-direction. (a) Taking the potential at the origin to be zero, write an expression for the potential at a general point (x, y, z). (b) At which point, the potential is 25 V? (c) If the potential at the origin is taken to be 100 V, what will be the expression for the potential at a general point? (d) What will be the potential at the origin if the potential at infinity is taken to be zero? Is it practical to choose the potential at infinity to be zero?
Draw equipotential surfaces corresponding to a uniform electric field in the z-directions.
Answer the following question.
Prove that the average energy density of the oscillating electric field is equal to that of the oscillating magnetic field.
A charge Q is applied to a conducting sphere of radius R. At the sphere's centre, the electric potential and electric field are respectively
