Advertisements
Advertisements
Question
Two charges of magnitudes −2Q and +Q are located at points (a, 0) and (4a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘3a’ with its centre at the origin?
Solution
Gauss’ theorem states that the electric flux through a closed surface enclosing a charge is equal to (1/ε0) times the magnitude of the charge enclosed.
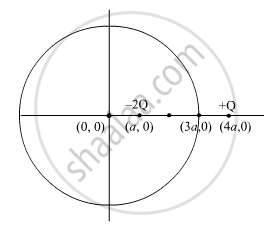
The sphere encloses a charge of -2Q thus, `phi 2Q/epsilon_0`
APPEARS IN
RELATED QUESTIONS
Define electric flux.
Consider a uniform electric field E = 3 × 103 `bbhat i` N/C.
- What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane?
- What is the flux through the same square if the normal to its plane makes a 60° angle with the x-axis?
Given a uniform electric filed \[\vec{E} = 4 \times {10}^3 \ \hat{i} N/C\]. Find the flux of this field through a square of 5 cm on a side whose plane is parallel to the Y-Z plane. What would be the flux through the same square if the plane makes a 30° angle with the x-axis?
A charge q is placed at the centre of the open end of a cylindrical vessel (see the figure). The flux of the electric field through the surface of the vessel is ____________ .

Electric charges are distributed in a small volume. The flux of the electric field through a spherical surface of radius 10 cm surrounding the total charge is 25 V m. The flux over a concentric sphere of radius 20 cm will be _____________ .
The electric field in a region is given by `vec"E"` = 5 `hatk`N/C. Calculate the electric flux Through a square of side 10.0 cm in the following cases
- The square is along the XY plane
- The square is along XZ plane
- The normal to the square makes an angle of 45° with the Z axis.
The electric flux through the surface ______.
 |
 |
 |
 |
| (i) | (ii) | (iii) | (iv) |
An electric charge q is placed at the center of a cube of side ℓ. The electric flux on one of its faces will be ______.
The electric charges are distributed in a small volume. The flux of the electric field through a spherical surface of radius 10 cm surrounding the total charge is 20 V-m. The flux over a concentric sphere of radius 20 cm will be ______.
