Advertisements
Advertisements
Question
Consider the situation of the previous problem. A charge of −2.0 × 10−4 C is moved from point A to point B. Find the change in electrical potential energy UB − UA for the cases (a), (b) and (c).
Solution
Given:
Magnitude of charge, q = −2.0 × 10−4 C
(a) The electric field is along the x direction.
Thus, potential difference between (0, 0) and (4, 2),
dV = −E.dx = −20 × 4 = −80 V
Potential energy (UB − UA) between the points = dV × q
⇒ UB − UA = (−80) × (−2.0 × 10−4)
⇒ UB − UA = 160 × 10−4 = 0.016 J
(b) A = (4 m, 2m), B = (6 m, 5 m)
dV = −E.dx = − 20 × 2 = −40 V
Potential energy (UB − UA) between the points = dV × q
⇒ UB − UA = (−40) × (−2 × 10−4)
⇒ UB − UA = 80 × 10−4 = 0.008 J
(c) A = (0, 0) B = (6m, 5m)
dV = −E.dx = −20 × 6 = −120 V
Potential energy (UB − UA) between the points A and B = dV × q
⇒ UB − UA = (−120) × (−2 × 10−4)
⇒ UB − UA = 240 × 10−4 = 0.024 J
APPEARS IN
RELATED QUESTIONS
The figure shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?

An infinite line charge produces a field of 9 × 104 N/C at a distance of 2 cm. Calculate the linear charge density.
Show that if we connect the smaller and the outer sphere by a wire, the charge q on the former will always flow to the latter, independent of how large the charge Q is.
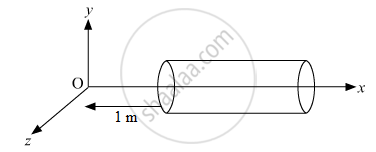
A hollow cylindrical box of length 0.5 m and area of cross-section 25 cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by `vecE = 20 xhati` where E is NC−1 and x is in metres. Find
(i) Net flux through the cylinder.
(ii) Charge enclosed by the cylinder.
Can a gravitational field be added vectorially to an electric field to get a total field?
If a body is charged by rubbing it, its weight
The electric field and the electric potential at a point are E and V, respectively.
Electric potential decreases uniformly from 120 V to 80 V, as one moves on the x-axis from x = −1 cm to x = +1 cm. The electric field at the origin
(a) must be equal to 20 Vcm−1
(b) may be equal to 20 Vcm−1
(c) may be greater than 20 Vcm−1
(d) may be less than 20 Vcm−1
Which of the following quantities does not depend on the choice of zero potential or zero potential energy?
A 10-cm long rod carries a charge of +50 μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both ends of the rod.
A ball of mass 100 g and with a charge of 4.9 × 10−5 C is released from rest in a region where a horizontal electric field of 2.0 × 104 N C−1 exists. (a) Find the resultant force acting on the ball. (b) What will be the path of the ball? (c) Where will the ball be at the end of 2 s?
A block of mass m with a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k, as shown in the figure. A horizontal electric field E, parallel to the spring, is switched on. Find the amplitude of the resulting SHM of the block. 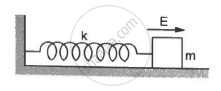
An electric field of 20 NC−1 exists along the x-axis in space. Calculate the potential difference VB − VA where the points A and B are
(a) A = (0, 0); B = (4 m, 2m)
(b) A = (4 m, 2 m); B = (6 m, 5 m)
(c) A = (0, 0); B = (6 m, 5 m)
Do you find any relation between the answers of parts (a), (b) and (c)?
An electric field \[\vec{E} = \vec{i}\] Ax exists in space, where A = 10 V m−2. Take the potential at (10 m, 20 m) to be zero. Find the potential at the origin.
When 1014 electrons are removed from a neutral metal sphere, the charge on the sphere becomes ______.
Two similar spheres having +Q and -Q charges are kept at a certain distance. F force acts between the two. If at the middle of two spheres, another similar sphere having +Q charge is kept, then it experiences a force in magnitude and direction as ______.
