Advertisements
Advertisements
प्रश्न
An electric field \[\vec{E} = ( \vec{i} 20 + \vec{j} 30) {NC}^{- 1}\] exists in space. If the potential at the origin is taken to be zero, find the potential at (2 m, 2 m).
उत्तर
Given:
\[\vec{E} = ( \vec{i} 20 + \vec{j} 30) \] N/C
\[\vec{r} = (2 \vec{i} + 2 \vec{j} )\]
So,
\[V = - \vec{E} . \vec{r}\]
\[\Rightarrow V = - ( \vec{i} 20 + 30 \vec{j} ) . (2 \vec{i} + 2 \vec{j} )\]
\[ \Rightarrow V = - (2 \times 20 + 2 \times 30) = - 100\] V
APPEARS IN
संबंधित प्रश्न
The charge on a proton is +1.6 × 10−19 C and that on an electron is −1.6 × 10−19 C. Does it mean that the electron has 3.2 × 10−19 C less charge than the proton?
When the separation between two charges is increased, the electric potential energy of the charges
The electric field at the origin is along the positive x-axis. A small circle is drawn with the centre at the origin, cutting the axes at points A, B, C and D with coordinates (a, 0), (0, a), (−a, 0), (0, −a), respectively. Out of the points on the periphery of the circle, the potential is minimum at
If a body is charged by rubbing it, its weight
A point charge q is rotated along a circle in an electric field generated by another point charge Q. The work done by the electric field on the rotating charge in one complete revolution is
A 10-cm long rod carries a charge of +50 μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both ends of the rod.
A wire is bent in the form of a regular hexagon and a total charge q is distributed uniformly on it. What is the electric field at the centre? You may answer this part without making any numerical calculations.
A particle of mass m and charge q is thrown at a speed u against a uniform electric field E. How much distance will it travel before coming to momentary rest ?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How much is the work done by the electric force on the particle during this period?
12 J of work has to be done against an existing electric field to take a charge of 0.01 C from A to B. How much is the potential difference VB − VA?
Find the magnitude of the electric field at the point P in the configuration shown in the figure for d >> a.
Which of the following methods can be used to charge a metal sphere positively without touching it? Select the most appropriate.
The surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the center of the disc is `sigma/(2∈_0)`. With respect to the field at the center, the electric field along the axis at a distance R from the center of the disc ______.
The electric field intensity produced by the radiations coming from 100 W bulb at 3 m distance is E. The electric field intensity produced by the radiations coming from 50 W bulb at the same distance is:
The Electric field at a point is ______.
- always continuous.
- continuous if there is no charge at that point.
- discontinuous only if there is a negative charge at that point.
- discontinuous if there is a charge at that point.
Five charges, q each are placed at the corners of a regular pentagon of side ‘a’ (Figure).
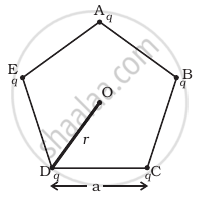
(a) (i) What will be the electric field at O, the centre of the pentagon?
(ii) What will be the electric field at O if the charge from one of the corners (say A) is removed?
(iii) What will be the electric field at O if the charge q at A is replaced by –q?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its corners?
