Advertisements
Advertisements
प्रश्न
Find the magnitude of the electric field at the point P in the configuration shown in the figure for d >> a.
उत्तर
Taking
\[\text{ So}, E = E_1 \cos \theta + E_2 cos\theta\]
\[ = E_1 cos\theta + E_2 cos\theta\]
\[ = 2 E_1 \cos \theta\]
\[ = 2 . \frac{1}{4\pi \in_0} . \frac{qa}{( d^2 + a^2 )^{3/2}}\]
\[ = \frac{1}{4\pi \in_0} . \frac{p}{d^3} [\text{ since } a < < d]\]

Notes
Figure is missing in the question .
APPEARS IN
संबंधित प्रश्न
Show that if we connect the smaller and the outer sphere by a wire, the charge q on the former will always flow to the latter, independent of how large the charge Q is.
Consider a system of n charges q1, q2, ... qn with position vectors `vecr_1,vecr_2,vecr_3,...... vecr_n`relative to some origin 'O'. Deduce the expression for the net electric field`vec E` at a point P with position vector `vecr_p,`due to this system of charges.
The charge on a proton is +1.6 × 10−19 C and that on an electron is −1.6 × 10−19 C. Does it mean that the electron has 3.2 × 10−19 C less charge than the proton?
Why does a phonograph record attract dust particles just after it is cleaned?
When the separation between two charges is increased, the electric potential energy of the charges
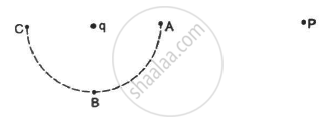
Consider the situation in the figure. The work done in taking a point charge from P to Ais WA, from P to B is WB and from P to C is WC.
Electric potential decreases uniformly from 120 V to 80 V, as one moves on the x-axis from x = −1 cm to x = +1 cm. The electric field at the origin
(a) must be equal to 20 Vcm−1
(b) may be equal to 20 Vcm−1
(c) may be greater than 20 Vcm−1
(d) may be less than 20 Vcm−1
The electric field in a region is directed outward and is proportional to the distance rfrom the origin. Taking the electric potential at the origin to be zero,
A 10-cm long rod carries a charge of +50 μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both ends of the rod.
A wire is bent in the form of a regular hexagon and a total charge q is distributed uniformly on it. What is the electric field at the centre? You may answer this part without making any numerical calculations.
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. Find the electric force and the force of gravity acting on this particle. Can one of these forces be neglected in comparison with the other for approximate analysis?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How long will it take for the particle to travel a distance of 40 cm?
Consider the situation of the previous problem. A charge of −2.0 × 10−4 C is moved from point A to point B. Find the change in electrical potential energy UB − UA for the cases (a), (b) and (c).
An electric field \[\vec{E} = ( \vec{i} 20 + \vec{j} 30) {NC}^{- 1}\] exists in space. If the potential at the origin is taken to be zero, find the potential at (2 m, 2 m).
An electric field \[\vec{E} = \vec{i}\] Ax exists in space, where A = 10 V m−2. Take the potential at (10 m, 20 m) to be zero. Find the potential at the origin.
The electric potential existing in space is \[\hspace{0.167em} V(x, y, z) = A(xy + yz + zx) .\] (a) Write the dimensional formula of A. (b) Find the expression for the electric field. (c) If A is 10 SI units, find the magnitude of the electric field at (1 m, 1 m, 1 m).
Consider a region inside which, there are various types of charges but the total charge is zero. At points outside the region ______.
Two similar spheres having +Q and -Q charges are kept at a certain distance. F force acts between the two. If at the middle of two spheres, another similar sphere having +Q charge is kept, then it experiences a force in magnitude and direction as ______.
