Advertisements
Advertisements
Question
Construct a regular hexagon of side 4 cm. Construct a circle circumscribing the hexagon.
Solution
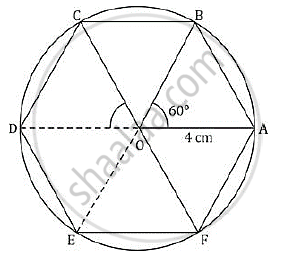
Steps of construction:
- Draw a circle of radius 4 cm with centre O.
- Since the interior angle of regular hexagon is 60°, draw radii OA and OB such that ∠AOB = 60°.
- Cut off arcs BC, CD, EF and each equal to arc AB on given circle.
- Join AB, BC, CD, DE, EF, FA to get required regular hexagon ABCDEF in a given circle.
The circle is the required circumcircle, circumscribing the hexagon.
APPEARS IN
RELATED QUESTIONS
Use ruler and compasses only for the following questions. All constructions lines and arcs must be clearly shown
Construct a ABC in which BC = 6.5 cm, ABC = 60°, AB = 5 cm.
Using ruler and compass only, construct a ΔABC such that BC = 5 cm and AB = 6.5
cm and ∠ABC = 120°
1) Construct a circum-circle of ΔABC
2) Construct a cyclic quadrilateral ABCD, such that D is equidistant from AB and BC.
Construct a ΔABC with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incircle.
Using a ruler and compasses only:
1) Construct a triangle ABC with the following data: AB = 3.5 cm, BC = 6 cm and ABC = 120°
2) In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
3) Measure ∠BCP.
Construct a triangle ABC in which base BC = 6 cm, AB = 5.5 cm and ∠ABC = 120°.
Construct a circle circumscribing the triangle ABC.
Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Using ruler and compasses only, construct and equilateral triangle with side 4.5 cm. Draw a circumcircle of this triangle and measure its radius.
Draw a circle of radius 4.5 cm. Take a point Pon its circumference. Construct a tangent to the circle at P without using the centre.
Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
What is the relation between the distances OA, OB and OC?
In triangle ABC, ∠ABC = 90°, AB = 6 cm, BC = 7.2 cm and BD is perpendicular to side AC. Draw circumcircle of triangle BDC and then state the length of the radius of this circumcircle drawn.
Ruler and compasses only may be used in this question. All constructions lines and arcs must be clearly shown, and the be sufficient length and clarity to permit assessment:
(i) Construct a triangle ABC, in which AB = 9 cm, BC = 10 cm and angle ABC = 45°.
(ii) Draw a circle, with center A and radius 2.5 cm. Let it meet AB at D.
(iii) Construct a circle to touch the circle with center A externally at D and also to touch the line BC.
