Advertisements
Advertisements
Question
Cubes A, B, C having edges 18 cm, 24 cm and 30 cm respectively are melted and moulded into a new cube D. Find the edge of the bigger cube D.
Solution
\[\text { We have the following: } \]
\[\text { Length of the edge of cube A = 18 cm }\]
\[\text { Length of the edge of cube B = 24 cm }\]
\[\text { Length of the edge of cube C = 30 cm }\]
\[\text { The given cubes are melted and moulded into a new cube D }. \]
\[\text { Hence, volume of cube D = volume of cube A + volume of cube B + volume of cube C }\]
\[ =\text { (side of cube A ) }^3 + \text { (side of cube B })^3 + \text { (side of cube C })^3 \]
\[ = {18}^3 + {24}^3 + {30}^3 \]
\[ = 5832 + 13824 + 27000\]
\[ = 46656 {cm}^3 \]
\[\text { Suppose that the edge of the new cube D = x }\]
\[ \Rightarrow x^3 = 46656\]
\[ \Rightarrow x = \sqrt[3]{46656} = 36 cm\]
\[ \therefore \text { The edge of the bigger cube D is 36 } cm .\]
APPEARS IN
RELATED QUESTIONS
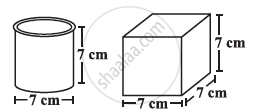
Describe how the two figures at the right are alike and how they are different. Which box has larger lateral surface area?
If each edge of a cube is doubled, how many times will its volume increase?
A cube A has side thrice as long as that of cube B. What is the ratio of the volume of cube A to that of cube B?
Suppose that there are two cubes, having edges 2 cm and 4 cm, respectively. Find the volumes V1and V2 of the cubes and compare them.
Find the surface area of a cube whose edge is 27 cm.
Find the cost of sinking a tubewell 280 m deep, having diameter 3 m at the rate of Rs 3.60 per cubic metre. Find also the cost of cementing its inner curved surface at Rs 2.50 per square metre.
A solid cube of side 12 cm is cut into 8 identical cubes. What will be the side of the new cube? Also, find the ratio between the surface area of the original cube and the total surface area of all the small cubes formed.
The base of a rectangular container is a square of side 12 cm. This container holds water up to 2 cm from the top. When a cube is placed in the water and is completely submerged, the water rises to the top and 224 cm3 of water overflows. Find the volume and surface area of the cube.
If the length of the diagonal of a cube is `6sqrt(3)` cm, then the length of the edge of the cube is 3 cm.
A cube of side 5 cm is painted on all its faces. If it is sliced into 1 cubic centimetre cubes, how many 1 cubic centimetre cubes will have exactly one of their faces painted?
