Advertisements
Advertisements
Question
D and E divides sides BC and CA of a triangle ABC in the ratio 2 : 3 respectively. Find the position vector of the point of intersection of AD and BE and the ratio in which this point divides AD and BE.
Solution
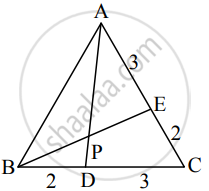
Let AD and BE intersect at P.
Let A, B, C, D, E, P have position vectos `bar"a", bar"b", bar"c", bar"d", bar"e", bar"p"` respectively.
D and E divide segments BC and CA internally in the ratio 2 : 3.
By the section formula for internal division,
`bar"d" = (2bar"c" + 3bar"b")/(2 + 3)`
∴ `5bar"d" = 2bar"c" + 3bar"b"` ....(1)
and `bar"e" = (2bar"a" + 3bar"c")/(2 + 3)`
∴ `5bar"e" = 2bar"a" + 3bar"c"` ....(2)
From (1), `5bar"d" - 3bar"b" = 2bar"c"` ...[both side multiply by 3]
∴ `15bar"d" - 9bar"b" = 6bar"c"`
From (2), `5bar"e" - 2bar"a" = 3bar"c"` ...[both side multiply by 2]
∴ `10bar"e" - 4bar"a" = 6bar"c"`
Equating both values of `6bar"c"`, we get
`15bar"d" - 9bar"b" = 10bar"e" - 4bar"a"`
∴ `15bar"d" + 4bar"a" = 10bar"e" + 9bar"b"`
∴ `(15bar"d" + 4bar"a")/(15 + 4) = (10bar"e" + 9bar"b")/(10 + 9)`
L.H.S is the position vector of the point which divides segment AD internally in the ratio 15 : 4
R.H.S is the position vector of the point which divides segment BE internally in the ratio 10 : 9
But P is the point of intersection of AD and BE
∴ P divides AD internally in the ratio 15 : 4 and P divides BE internally in the ratio 10 : 9
Hence, the position vector of the point of interaction of AD and BE is
`bar"p" = (15bar"d" + 4bar"a")/19 = (10bar"e" + 9bar"b")/19`
and it divides AD internally in the ratio 15 : 4 and BE internally in the ratio 10 : 9.
APPEARS IN
RELATED QUESTIONS
If `bar("AB") = 2hat"i" + hat"j" - 3hat"k"`, and A(1, 2 ,−1) is given point then coordinates of B are ______.
Find the distance from (4, −2, 6) to the XZ- plane
The co-ordinates of the foot of perpendicular drawn from origin to the plane 2x - y + 5z - 3 = 0 are ______.
If `bar"a", bar"b", bar"c"` are the three non-coplanar vectors and `bar"p", bar"q", bar"r"` are defined by the relations `bar"p" = (bar"b" xx bar"c")/([(bar"a", bar"b", bar"c")]), bar"q" = (bar"c" xx bar"a")/([(bar"a", bar"b", bar"c")]), bar"r" = (bar"a" xx bar"b")/([(bar"a", bar"b", bar"c")])` then `(bar"a" + bar"b")* bar"p" + (bar"b" + bar"c") * bar"q" + (bar"c" + bar"a") * bar"r"` = ______.
The co-ordinates of a point on the line x = 4y + 5, z = 3y – 6 at a distance `3sqrt(26)` from the point (5, 0, –6) are ______.
If P1 and P2 are the lengths of the perpendiculars from the points (2, 3, 4) and (1, 1, 4) respectively from the plane 3x – 6y + 2z + 11 = 0, then P1 and P2 are the roots of the equation ______.
The equation of set points P such that PA2 + PB2 = 2K2, where A and B are the points (3, 4, 5) and (–1, 3, –7), respectively is ______.
The foot of the perpendicular drawn from the origin to a plane is the point (1, –3, 1). What is the intercept cut on the x-axis by the plane?
Three vertices of a parallelogram ABCD are A ( 3, –1, 2), B (1, 2, –4) and C (–1, 1, 2). The coordinates of fourth vertex D are ______.
The equation of the plane containing the line `(x + 1)/(-3) = (y - 3)/2 = (z + 2)/1` and the point (0, 7, –7), is ______.
The co-ordinates of the foot of perpendicular from the point A (1, 1, 1) on the line joining the points B (1, 4, 6) and C (5, 4, 4) are ______.
The distance of the point (1, –2, 3) from the plane x – y + z = 5 measured parallel to the line `x/2 = y/3 = (z - 1)/(-6)` is ______.
If the distance of points `2hati + 3hatj + λhatk` from the plane `r.(3hati + 2hatj + 6hatk)` = 13 is 5 units, then λ = ______.
The equation of the plane passing through the points (1, 2, 3), (–1, 4, 2) and (3, 1, 1) is ______.
A line makes angles α, β, γ with the positive directions of coordinate axes, then find the value of sin2α + sin2β + sin2γ.
