Advertisements
Advertisements
Question
D और E क्रमश : ∆ABC की भुजा AB और AC के मध्य-बिंदु है तथा O भुजा BC पर कोई बिंदु है। O को A से मिलाया जाता है। यदि P और Q क्रमश : OB और OC के मध्य-बिंदु हैं, तो DEQP है एक ______।
Options
वर्ग
आयत
समचतुर्भुज
समांतर चतुर्भुज
Solution
D और E क्रमश : ∆ABC की भुजा AB और AC के मध्य-बिंदु है तथा O भुजा BC पर कोई बिंदु है। O को A से मिलाया जाता है। यदि P और Q क्रमश : OB और OC के मध्य-बिंदु हैं, तो DEQP है एक समांतर चतुर्भुज।
स्पष्टीकरण -
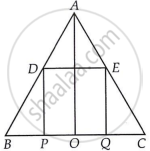
ΔABC में, D और E क्रमश : AB और AC भुजाओं के मध्य-बिंदु हैं।
मध्य-बिंदु प्रमेय द्वारा,
DE || BC ...(i)
DE = `1/2` BC
फिर, DE = `1/2` [BP + PO + OQ + QC]
DE = `1/2` [2PO + 2OQ] ...[चूंकि, P और Q क्रमश : OB और OC के मध्य-बिंदु हैं।]
⇒ DE = PO + OQ
⇒ DE = PQ
अब, ΔAOC में, Q और E क्रमश : OC और AC के मध्य-बिंदु हैं।
∴ EQ || AO और EQ = `1/2` AO [मध्य-बिंदु प्रमेय द्वारा] ...(iii)
इसी प्रकार, ΔABO में,
PD || AO और PD = `1/2` AO [मध्य-बिंदु प्रमेय द्वारा] ...(iv)
समीकरण (iii) और (iv) से,
EQ || PD और EQ = PD
समीकरण (i) और (ii) से,
DE || BC (या DE || PQ) और DE = PQ
अतः, DEQP एक समांतर चतुर्भुज है।
APPEARS IN
RELATED QUESTIONS
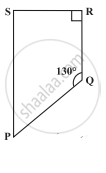
आकृति में ∠P तथा ∠S की माप ज्ञात कीजिए यदि `overline("SP")||overline("RQ")` है। (यदि आप m∠R, ज्ञात करने हैं, तो क्या m∠P को ज्ञात करने की एक से अधिक विधि है?)
बताइए कैसे एक वर्ग एक चतुर्भुज है।
यदि APB और CQD दो समांतर रेखाएँ हैं, तो कोणों APQ, BPQ, CQP और PQD के समद्विभाजक बनाते हैं
एक समचतुर्भुज की भुजाओं के मध्य-बिंदुओं को, एक ही क्रम में, मिलाने पर बनने वाली आकृति होती है
समांतर चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर प्रतिच्छेद करते हैं। यदि ∠DAC = 32° और ∠AOB = 70° हैं तो ∠DBC बराबर है
9 बजे घड़ी की घंटे तथा मिनट की सूइयों के बीच में बने कोणों के माप हैं:
आकृति में, अधिक कोणों की संख्या है-

यदि दो कोणों का योग एक अधिक कोण के बराबर है, तो निम्नलिखित में से कौन-सा विकल्प संभव नहीं है?
आकृति के भाग में, दी हुई सूचना का प्रयोग करके समकोण लिखिए-
BA ⊥BD
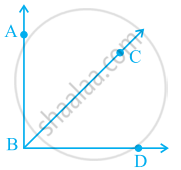
आकृति के भाग में, दी हुई सूचना का प्रयोग करके समकोण लिखिए-
OP ⊥ AB