Advertisements
Advertisements
Question
Deduce an expression for the frequency of revolution of a charged particle in a magnetic field and show that it is independent of velocity or energy of the particle.
Solution
When a charged particle with charge q moves inside a magnetic field `vecB`with velocity v, it experiences a force, which is given by:
`vecF=q(vecvxxvecB)`
Here, `vecv` is perpendicular to `vecB`,`vecF`is the force on the charged particle which acts as the centripetal force and makes it move along a circular path.
Let m be the mass of the charged particle and r be the radius of the circular path.
`:.q(vecvxxvecB)=(mv^2)/r`
v and B are at right angles:
`:.qvB=(mv^2)/r`
`r=(mv)/(Bq)`
Time period of circular motion of the charged particle can be calculated as shown below:
`T=(2pir)/v`
`=(2pi)/v(mv)/(Bq)`
`T=(2pim)/(Bq)`
∴ Angular frequency is
`omega=(2pi)/T`
|
`:.omega=(Bq)/m` |
Therefore, the frequency of the revolution of the charged particle is independent of the velocity or the energy of the particle.
APPEARS IN
RELATED QUESTIONS
State the underlying principle of a cyclotron. Write briefly how this machine is used to accelerate charged particles to high energies
A deuteron and a proton are accelerated by the cyclotron. Can both be accelerated with the same oscillator frequency? Give reason to justify your answer.
An α-particle and a proton are released from the centre of the cyclotron and made to accelerate.
(i) Can both be accelerated at the same cyclotron frequency?
Give reason to justify your answer.
(ii) When they are accelerated in turn, which of the two will have higher velocity at the exit slit of the does?
A cyclotron is used to accelerate protons to a kinetic energy of 5 MeV. If the strength of magnetic field in the cyclotron is 2T, find the radius and the frequency needed for the applied alternating voltage of the cyclotron. (Given : Velocity of proton= `3xx10^7 m//s`)
Figure shows a rod PQ of length 20.0 cm and mass 200 g suspended through a fixed point O by two threads of lengths 20.0 cm each. A magnetic field of strength 0.500 T exists in the vicinity of the wire PQ, as shown in the figure. The wires connecting PQ with the battery are loose and exert no force on PQ. (a) Find the tension in the threads when the switch S is open. (b) A current of 2.0 A is established when the switch S is closed. Find the tension in the threads now.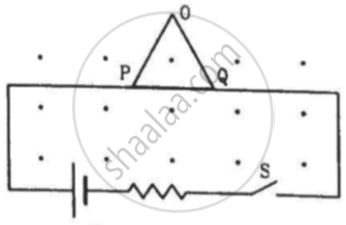
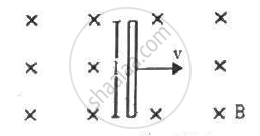
A conducting wire of length l, lying normal to a magnetic field B, moves with a velocity v,as shown in the figure. (a) Find the average magnetic force on a free electron of the wire. (b) Due to this magnetic force, electrons concentrate at one end, resulting in an electric field inside the wire. The redistribution stops when the electric force on the free electrons balances the magnetic force. Find the electric field developed inside the wire when the redistribution stops. (c) What potential difference is developed between the ends of the wire?
Assertion: The frequency of circular motion of a charged particle in cyclotron is independent of the mass of the particle.
Reason: Greater the mass of the particle less will be the frequency of the particle.
The cyclotron was designed by ______
In a cyclotron, a charged particle ______.
