Advertisements
Advertisements
प्रश्न
Deduce an expression for the frequency of revolution of a charged particle in a magnetic field and show that it is independent of velocity or energy of the particle.
उत्तर
When a charged particle with charge q moves inside a magnetic field `vecB`with velocity v, it experiences a force, which is given by:
`vecF=q(vecvxxvecB)`
Here, `vecv` is perpendicular to `vecB`,`vecF`is the force on the charged particle which acts as the centripetal force and makes it move along a circular path.
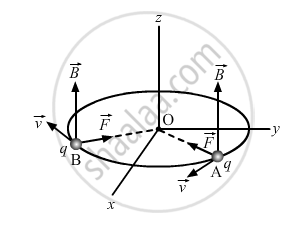
Let m be the mass of the charged particle and r be the radius of the circular path.
`:.q(vecvxxvecB)=(mv^2)/r`
v and B are at right angles:
`:.qvB=(mv^2)/r`
`r=(mv)/(Bq)`
Time period of circular motion of the charged particle can be calculated as shown below:
`T=(2pir)/v`
`=(2pi)/v(mv)/(Bq)`
`T=(2pim)/(Bq)`
∴ Angular frequency is
`omega=(2pi)/T`
|
`:.omega=(Bq)/m` |
Therefore, the frequency of the revolution of the charged particle is independent of the velocity or the energy of the particle.
APPEARS IN
संबंधित प्रश्न
Draw a neat labelled diagram for the construction of 'cyclotron'
State the underlying principle of a cyclotron. Write briefly how this machine is used to accelerate charged particles to high energies
Explain the principle and working of a cyclotron with the help of a schematic diagram. Write the expression for cyclotron frequency.
Which of the following particles will describe the smallest circle when projected with the same velocity perpendicular to a magnetic field?
(a) An electron moves along a circle of radius 1 m in a perpendicular magnetic field of strength 0.50 T. What would be its speed? Is it reasonable? (b) If a proton moves along a circle of the same radius in the same magnetic field, what would be its speed?
A cyclotron's oscillator frequency is 10 MHz. What should be the operating magnetic field for accelerating protons? If the radius of its 'dees' is 60 cm, calculate the kinetic energy (in MeV) of the proton beam produced by the accelerator.
A particle of mass m is moving in a circular path of constant radius r such that, its centripetal acceleration ac is varying with time t as ac = k2rt2, where k is a constant. The power delivered to the particle by the forces acting on it is ______.
The cyclotron was designed by ______
Verify that the cyclotron frequency ω = eB/m has the correct dimensions of [T]–1.
Describe the motion of a charged particle in a cyclotron if the frequency of the radio frequency (rf) field were doubled.
