Question

Derive an expression for maximum work in isothermal reversible expansion of two moles of an ideal gas.

Derive an expression for maximum work obtainable during isothermal reversible expansion of an ideal gas from initial volume (V₁) to final volume (V₂).

Answer 1

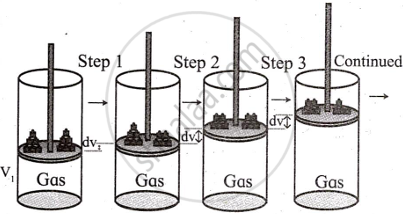
1. Consider the expansion of ‘n’ moles of an ideal gas enclosed in a cylinder fitted with a weightless and
   frictionless piston at a constant temperature T.
2. Let the pressure of the gas be P, which is equal to the external pressure.
3. Let the external pressure be reduced by an infinitesimally small amount dp so that the new external pressure becomes (P − dp).
4. Let the corresponding small increase in volume by dv. 
5. Therefore, the amount of work done in the expansion of the gas, dw = −[(p dp)dv] = −[pdv − dp.dv]    ..(i)
6. Since dp and dv are very small, their product (dp.dv) will be much smaller and can be neglected ∴ dw = −pdv  ...(ii)

7. During expansion of the gas, if the initial volume V₁ changes to volume V₂ then total amount of work alone (Wmax) can be obtained by integrating the work, dw between the two limits, V₁ and V₂.

`therefore "W"_"max" = int_("v"_2)^("v"_1) - dw`

= `int_("v"_1)^("v"_2) - pdv`   ...(iii)

But pv = nRT (Ideal gas Equation for n moles of a gas)

`therefore "p" = "nRT"/"v"`

Substitute pressure value in equation (iii) 

`therefore "W" _"max" = int_("v"_1)^("v"_2) - ("nRT")/"v" "dv"`

= `"nRT" int_("v"_1)^("v"_2) "dv"/"v"`  (n,R,T are constant)

= `-"nRT"  ["log v"]_("v"_1)^("v"_2)`

= `-"nRT"  "ln" "v"_2/"v"_1`

`therefore "W"_"max" = -2.303 "nRT"  "log" "v"_2/"v"_1`

(In = 2.303 log₁₀)  ...(iv)