Advertisements
Advertisements
Question
Derive an expression for acceleration due to gravity at depth ‘d’ below the earth’s surface.
Solution
Let M be mass of the earth, R be the radius of the earth
gd be gravitational acceleration at depth 'd ' from the earth surface
g be gravitational acceleration on the earth surfaces.
ρ be the density of the earth.
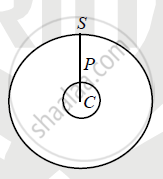
‘P’ be the point inside the earth at depth 'd ' from earth surfaces.
∴ CS-CP=d, ∴ CP=R-d .............(1) (since CS=R)
`g=(GM)/R^2`,
`therefore g=(G4/3piR^3rho)/R^2`
`therefore g=(4GpiRrho)/3` ....(2)
gd = acceleration due to gravity at depth 'd '
`g_d=(Gxx"Mass of the sphere with radius CP")/(CP^2)`
`thereforeg_d=(G4/3piCP^3rho)/(CP^2)`
`thereforeg_d=(4GpiCPrho)/3` .... (3)
Dividing eq. (3) by eq. (2)
`g_d/g=(CP)/R=(R-d)/R`
`therefore g_d=g(1-d/R)`
APPEARS IN
RELATED QUESTIONS
Derive an expression for critical velocity of a satellite revolving around the earth in a circular orbit.
A sonometer wire vibrates with frequency n1 in air under suitable load of specific gravity of . When the load is immersed in water, the frequency of vibration of wire n2 will be .........
What is the decrease in weight of a body of mass 600kg when it is taken in a mine of depth 5000m?
[ Radius of earth = 6400km, g = 9.8 m/s2 ]
A stone of mass 100 g attached to a string of length 50 cm is whirled in a vertical circle by giving velocity at lowest point as 7 m/s. Find the velocity at the highest point. [Acceleration due to gravity = 9.8 m/s2 ]
Io, one of the satellites of Jupiter, has an orbital period of 1.769 days and the radius of the orbit is 4.22 × 108 m. Show that the mass of Jupiter is about one-thousandth that of the sun.
A hole is drilled half way to the centre of the Earth. A body is dropped into the hole. How much will it weigh at the bottom of the hole if the weight of the body on the Earth’s surface is 350 N?
Prove that `g_h=g(1-"2h"/R)` where gh is the acceleration due to gravity at altitude h and h << R (R is the radius of the earth).
‘g’ is the acceleration due to gravity on the surface of the Earth and ‘R’ is the radius of the
Earth.
Show that acceleration due to gravity at height ‘h’ above the surface of the Earth is
`gh = g (R/(R+H))^2`
What is the decrease in weight of a body of mass 500 kg when it is taken into a mine of depth 1000 km? (Radius of earth R = 6400 km, g = 9.8 m/s2)
If the radius of the earth decreases by 1% without changing its mass, will the acceleration due to gravity at the surface of the earth increase or decrease? If so, by what per cent?
