Advertisements
Advertisements
Questions
Derive the relation between surface tension and surface energy per unit area.
Derive the relation between surface energy & surface tension.
Solution 1
Surface tension tries to decrease the surface area of a liquid. For increasing surface area, the work has to be done against the surface tension and it is stored in the surface molecules in the form of potential energy
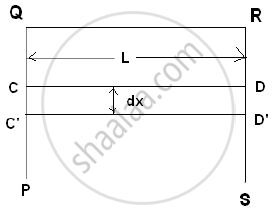
Consider a rectangular frame PQRS having a movable wire CD. Let QR = CD = L. If a soap film is formed on the frame CQRD, then the surface tension will try to pull the wire inward by a force F.
`"Surface tension" = "Force"/"free Length"`
F = Surface tension × Free length
∴ F = T × (2L)
If the wire is pulled out to C'D' through distance ‘dx’.
∴ Work done = F. dx
∴ W = T (2Ldx)
But increase in area = dA = 2Ldx
Surface energy is defined as the work done per unit area to increase the free surface area, under isothermal conditions.
`therefore "Surface energy"="Work done"/"Free surface area"=W/"dA"=(T(2Ldx))/(2Ldx)=T`
∴ Surface tension is also equal to the surface energy per unit area.
Solution 2

Consider a C-shaped frame of wire P'PSS'. It is fitted with a movable arm QR, as shown in Fig. This frame is dipped in a soap solution and then taken out. A film of soap solution will be formed within the boundaries PQRS of the frame.
Each arm of the frame experiences an inward force due to the film. Under the action of this force, the movable arm QR moves towards side PS so as to decrease the area of the film. If the length of QR is L, then this inward force F acting on it is given by
F = (T) × (2L) ...(1)
Since the film has two surfaces, the upper surface and the lower surface, the total length over which surface tension acts on QR is 2L. Imagine an external force F' (equal and opposite to F) applied isothermally (gradually and at constant temperature) to the arm QR so that it pulls the arm away and tries to increase the surface area of the film. The arm QR moves to Q'R' through a distance dx. Therefore, the work done against F, the force due to surface tension, is given by
dw = F'dx
Using equation (1),
dw = T (2Ldx)
But, 2Ldx = dA, increase in area of the two surfaces of the film. Therefore, dw = T(dA).
This work done in stretching the film is stored in the area dA of the film as its potential energy. This energy is called surface energy.
∴ Surface energy = T (dA) ...(2)
Thus, surface tension is also equal to the surface energy per unit area.
APPEARS IN
RELATED QUESTIONS
Answer in one sentence.
State the SI unit and dimensions of stress.
The radius of a soap bubble is blown up to double its value under isothermal conditions. If 'r' be the initial radius of the bubble, and T be the surface tension, then energy spent in doubling the radius is ______
Energy needed in breaking a drop of radius R into n drops each of radius r is given by ____________.
Assertion: If work done in increasing the size of a soap film from 10 cm x 4 cm to 10 cm x 8 cm is 2 x 10-4 J, then the surface tension is 5 x 10-4 N m-1.
Reason: Work done = Surface tension x increase in area.
If two identical mercury drops are combined to form a single drop, then its temperature will ____________.
Which one of the following statements is correct?
A metal wire of density 'p' floats on water surface horizontally. If it is NOT to sink in water then maximum radius of wire is proportional to ______.
(T = surface tension of water, g = gravitational acceleration)
Two spherical soap bubbles of radii r1 and r2 in vacuum coalesce under isothermal conditions. The resulting bubble has a radius R such that ____________.
A liquid drop having surface energy 'E' is spread into 216 droplets of same size. The final surface energy of the droplets is ____________.
The surface energy of a liquid drop is u. If it is sprayed into 1000 equal droplets, then its surface energy becomes ______.
If a million tiny droplets of water of the same radius coalesce into one larger drop, then the ratio of the surface energy of the large drop to the total surface energy of all the droplets will be ____________.
On the surface of the liquid in equilibrium, molecules of the liquid possess ____________.
Consider a process shown in the figure. During this process, the work done by the system ______.
A metal coin of thickness 'd' and density 'ρ' is floating on water of surface tension 'T'. The radius of the coin is ______.
g = acceleration due to gravity
One thousand small water drops of equal radii combine to form a big drop. The ratio of final surface energy to the total initial surface energy is ______.
The surface tension of a liquid is 10 N/m. If a thin film of the area 0.05 m2 is formed on a loop. Then the surface energy will be:
Prove that, equivalent S.I. unit of surface tension is J/m2.
Define the surface energy of the liquid.
