Question

Derive the expression for the work done in a volume change in a thermodynamic system.

Answer 1

Work done in volume changes: Consider a gas contained in the cylinder fitted with a movable piston. Suppose the gas is expanded quasi-statically by pushing the piston by a small distance dx. Since the expansion occurs quasi-statically the pressure, temperature and internal energy will have unique values at every instant.

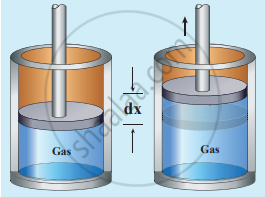
         Work done by the gas

The small work done by the gas on the piston

dW = Fdx ….........(1)

The force exerted by the gas on the piston F = PA.

Here A is the area of the piston and P is the pressure exerted by the gas on the piston.

Equation (1) can be rewritten as Work done by the gas

dW = PA dx …..........(2)

But Adx = dV= change in volume during this expansion process.

So the small work done by the gas during the expansion is given by

dW = PdV .........….(3)

dV is positive since the volume is increased. Here, dW is positive.

In general, the work done by the gas by increasing the volume from V_i to V_f is given by

W = `int_("V"_"i")^("V"_"f") "PdV"` ..........(4)

Suppose if the work is done on the system, then V_i > V_f. Then, W is negative.

Note here the pressure P is inside the integral in equation (4). It implies that while the system is doing work, the pressure need not be constant. To evaluate the integration we need to first express the pressure as a function of volume and temperature using the equation of state.