Advertisements
Advertisements
Question
Derive the relation between f and R for a spherical mirror.
Solution
- C be the center of curvature of the mirror
- F be the principal focus.
- Line CM is normal to the mirror at M.
- i be the angle of incidence
∠MCP = i and ∠MFP = 2 i
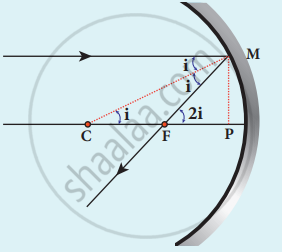
(a) Concave mirror
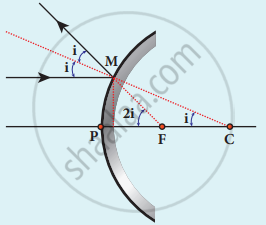
(b) Convex Mirror
ΔMCP,
tan i = `"PM"/"PC"`
ΔMFB, tan 2i = `"PM"/"PF"`
i = `"PM"/"PC" and "2i" = "PM"/"PF"`
`2"PM"/"PC" = "PM"/"PF"`; 2PF = PC
∵ PF = f
PC = R
2f = R (or) f = `"R"/2`
APPEARS IN
RELATED QUESTIONS
What are the Cartesian sign conventions for a spherical mirror?
An object of 4 cm height is placed at 6 cm in front of a concave mirror of radius of curvature 24 cm. Find the position, height, magnification and nature of the image.
Obtain the lens maker’s formula for a lens of refractive index n2 which is separating two media of refractive indices n1 and n3 on the left and right respectively.
Prove that a convex lens can only form a virtual, erect and diminished image.
A biconvex lens has focal length f and intensity of light I passing through it. What will be the focal length and intensity for portions of lenses obtained by cutting it vertically and horizontally as shown in the figure?

