Advertisements
Advertisements
Question
Determine whether the given set of points are collinear or not
(7, −2), (5, 1), (3, 4)
Solution
To prove that three points are collinear, sum of the distance between two pairs of points is equal to the third pair of points.
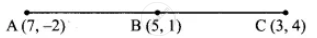
Distance AB = `sqrt((5 - 7)^2 + (1 + 2)^2`
= `sqrt((-2)^2 + (3)^2`
= `sqrt(4 + 9)`
= `sqrt(13)`
BC = `sqrt((3 - 5)^2 + (4 - 1)^2`
= `sqrt((-2)^2 + (3)^2`
= `sqrt(4 + 9)`
= `sqrt(13)`
AC = `sqrt((3 - 7)^2 + (4 + 2)^2`
= `sqrt((-4)^2 + (6)^2`
= `sqrt(16 + 36)`
= `sqrt(52)`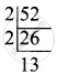
= `sqrt(2 xx 2 xx 13)`
= `2sqrt(13)`
AB + BC = AC
`sqrt(13) + sqrt(13) = 2sqrt(13)`
⇒ `2sqrt(13) = 2sqrt(13)`
∴ The given three points are collinear.
APPEARS IN
RELATED QUESTIONS
On a number line, co-ordinates of P, Q, R are 3, -5 and 6 respectively. State with reason whether the following statement is true or false.
d(P, Q) - d(P, R) = d(Q, R)
Co-ordinates of the pair of a point is given below. Hence find the distance between the pair.
3, 6
Co-ordinates of the pair of points are given below. Hence find the distance between the pair.
-9, -1
Co-ordinates of the pair of points are given below. Hence find the distance between the pair.
0, - 2
Co-ordinates of the pair of points are given below. Hence find the distance between the pair.
- 25, - 47
Show that the following points taken in order to form an isosceles triangle
A(5, 4), B(2, 0), C(−2, 3)
Show that the following points taken in order to form the vertices of a parallelogram
A(−7, −3), B(5, 10), C(15, 8) and D(3, −5)
The point whose ordinate is 4 and which lies on the y-axis is _______________
The distance between the point (5, −1) and the origin is _________
Find the distance with the help of the number line given below.

d(K, O)
