Advertisements
Advertisements
Question
Discuss the following case:
Source in motion and Observer at rest
- Source moves towards observer
- Source moves away from the observer
Advertisements
Solution
(a) Source moves towards die observer-
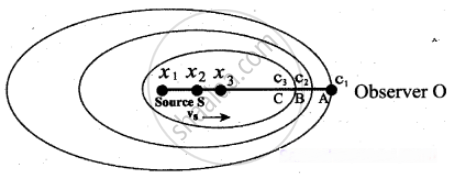
Source S moves towards an observer O (right) with velocity
Suppose a source S moves to the right (as shown in Figure) with a velocity vs and let the frequency of the sound waves produced by the source be fs. It is assumed that the velocity of sound in a medium is v.
Suppose a source S moves to the right (as shown in Figure) with a velocity vs and let the frequency of the sound waves produced by the source be fs. It is assumed that the velocity of sound in a medium is v.
The compression (sound wavefront) produced by the source S at three successive instants of time are shown in the Figure. When S is at position x1 the compression is at C1. When S is at position x2, the compression is at C2 and similarly for x3 and C3.
It is meant that the wavelength decreases when the source S moves towards the observer O. But frequency is inversely related to wavelength and therefore, frequency increases.
Calculation:
Let λ be the wavelength of the source S as measured by the observer when S is at position x1 and λ’ be the wavelength of the source observed by the observer when S moves to position x2.
Then the change in wavelength is ∆λ = λ – λ’ = vst, where t is the time taken by the source to travel between x1 and x2 Therefore,
λ’ = λ – vst … (1)
But t = \[\frac{λ}{v}\] … (2)
On substituting equations (2) in equation (1), we get.
`lambda' = lambda(1 - "v"_"s"/"v")`
Since frequency is inversely proportional to wavelength, we have
`"f"' = "v"_"s"/(lambda')` and f = `"v"_"s"/lambda`
Hence `"f"' = "f"/((1 - "v"_"s"/"v"))` ...(3)
Since, `"v"_"s"/"v"` << 1, by using the binomial expansion and retaining only first order in `"v"_"s"/"v"`, we get
`"f"' = "f"(1 + "v"_"s"/"v")` ...(4)
(b) Source moves away from the observer-
Since the velocity of the source is opposite in direction when compared to case (a), hence by changing the sign of the velocity of the source in the above case i.e., by substituting (vs → – v ) in equation (1), we get
`"f"' = "f"/((1 + "v"_"s"/"v"))` ....(5)
Using binomial expansion again, we get
`"f"' = "f"(1 - "v"_"s"/"v")` .....(6)
APPEARS IN
RELATED QUESTIONS
In discussing Doppler effect, we use the word "apparent frequency". Does it mean that the frequency of the sound is still that of the source and it is some physiological phenomenon in the listener's ear that gives rise to Doppler effect? Think for the observer approaching the source and for the source approaching the observer.
Answer briefly.
State the expression for apparent frequency when source of sound and listener are
- moving towards each other
- moving away from each other
A ship in a sea sends SONAR waves straight down into the seawater from the bottom of the ship. The signal reflects from the deep bottom bedrock and returns to the ship after 3.5 s. After the ship moves to 100 km it sends another signal which returns back after 2 s. Calculate the depth of the sea in each case and also compute the difference in height between two cases.
The difference between the apparent frequency of a source of sound as perceived by the observer during its approach and recession is 2% of the frequency of the source. If the speed of sound in air is 300 ms-1, then the velocity of the source is ______.
A source of sound is moving towards a stationary observer with velocity 'Vs' and then moves away with velocity 'Vs'. Assume that the medium through which the sound waves travel is at rest, if 'V' is the velocity of sound and 'n' is the frequency emitted by the source, then the difference between the apparent frequencies heard by the observer is ______.
A train whistling at constant frequency is moving towards a station at a constant speed V. The train goes past a stationary observer on the station. The frequency n ′ of the sound as heard by the observer is plotted as a function of time t (figure). Identify the expected curve.
A sitar wire is replaced by another wire of same length and material but of three times the earlier radius. If the tension in the wire remains the same, by what factor will the frequency change?
When a sound source of frequency n is approaching a stationary observer with velocity u than the apparent change in frequency is Δn1 and when the same source is receding with velocity u from the stationary observer than the apparent change in frequency is Δn2. Then ______.
The period of rotation of the sun at its equator is T and its radius is R. Then the Doppler wavelength shift expected for light with wavelength λ emitted from the edge of the sun's disc is: [c = speed of light]
The pitch of the whistle of an engine appears to drop by 20% of its original value when it passes a stationary observer. If the speed of sound in the air is 350 m/s, then the speed of the engine (in m/s) is ______.
