Advertisements
Advertisements
Question
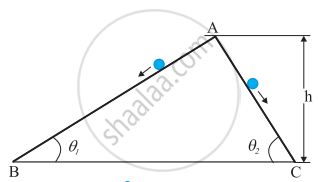
दो घर्षणरहित आनत पथ, जिनमें से एक की ढाल अधिक है। और दूसरे की ढाल कम है, बिंदु A पर मिलते हैं। बिंदु A से प्रत्येक पथ पर एक-एक पत्थर को विरामावस्था से नीचे सरकाया जाता है। क्या ये पत्थर एक ही समय पर नीचे पहुँचेंगे? क्या वे वहाँ एक ही चाल से पहुँचेंगे? व्याख्या कीजिए। यदि θ1 = 30°, θ2 = 60° और h= 10 m दिया है तो दोनों पत्थरों की चाल एवं उनके द्वारा नीचे पहुँचने में लिए गए समय क्या हैं?
Solution
चित्र से, तल AB की लंबाई, `"l"_1 = "h"/("sin" theta_1)`
इस तल पर नीचे की ओर पत्थर का त्वरण, a1 = g sin θ1
यदि इस तल पर नीचे पहुंचने में पत्थर द्वारा लिया गया समय t1 सेकंड हो तो,
`"s" = "ut" + 1/2 "at"^2` से
`"h"/("sin" theta_1) = 0 xx "t"_1 + 1/2 "g" "sin" theta_1 xx "t"_1^2`
सरल करने पर,
`"t"_1 = 1/("sin" theta_1) sqrt((2"h")/"g")`
= `1/("sin" 30^circ) sqrt((2 xx 10)/10)`
= `2sqrt2 "सेकंड"`
इसी प्रकार तल AC के लिए इस पर पत्थर के नीचे आने का समय
`"t"_2 = 1/("sin" theta_1) sqrt((2"h")/"g")`
= `1/("sin" 60^circ) sqrt((2 xx 10)/10)`
= `(2sqrt2)/sqrt3` सेकंड
अतः गति की समीकरण `"ν"^2 = "u"^2 + 2 "as"` से,
`"ν"^2 = 0 + 2 ("g" "sin" theta_1) xx "h"/("sin" theta_1) = 2"gh"`
अथवा पत्थर की B पर पहुँचने की चाल,
`"ν" = sqrt(2"gh")`
चूँकि यह पर निर्भर नहीं करती है, अतः AB तथा AC पर नीचे आने वाले पत्थर नीचे एक ही चाल से पहुंचेंगे जिसका मान
`"ν" = sqrt(2"gh")`
= `sqrt(2 xx 10 xx 10)`
= `10sqrt2`
= 10 × 1.41 m/s
= 14.1 m/s
APPEARS IN
RELATED QUESTIONS
कोई पिंड जो विरामावस्था में है, अचर त्वरण से एकविमीय गति करता है। इसको किसी t समय पर दी गई शक्ति अनुक्रमानुपाती है -
कोई व्यक्ति वजन कम करने के लिए 10 kg द्रव्यमान को 0.5 m की ऊंचाई तक 1000 बार उठाता है। मान लीजिए कि प्रत्येक बार द्रव्यमान को नीचे लाने में खोई हुई ऊर्जा क्षयित हो जाती है।
- वह गुरुत्वाकर्षण बल के विरुद्ध कितना कार्य करता है?
- यदि वसा 3.8 × 107 J ऊर्जा प्रति किलोग्राम आपूर्ति करता हो जो कि 20% दक्षता की दर से यांत्रिक ऊर्जा में परिवर्तित हो जाती है तो वह कितनी वसा खर्च कर डालेगा?
