Advertisements
Advertisements
Question
Draw a right angled Δ XYZ. Draw its medians and show their point of concurrence by G.
Solution

Steps of construction:
- Draw a right angled ∆XYZ.
- Draw the perpendicular bisector PQ of side YZ that intersect YZ at L.
- Join XL. XL is the median to the side YZ.
- Draw the perpendicular bisector TU of side ZX that intersect YZ at M.
- Join YM. YM is the median to side ZX.
- Draw the perpendicular bisector RS of side XY that intersect XY at N.
- Join ZN. ZN is the median to the side XY.
Hence, ∆XYZ is the required triangle in which medinas XL, YM and ZN to the sides YZ, ZX and XY respectively, intersect at G.
The point G is the centroid of ∆XYZ..
RELATED QUESTIONS
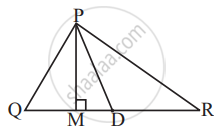
In ΔPQR, D is the mid-point of `bar(QR)`.
`bar(PM)` is ______.
PD is ______.
Is QM = MR?
Draw rough sketch for the following:
In ΔABC, BE is a median.
Draw rough sketch for the following:
In ΔPQR, PQ and PR are altitudes of the triangle.
Name the orthocentre of ∆PQR
The sides of a right angled triangle are in the ratio 5 : 12 : 13 and its perimeter is 120 units then, the sides are ______________
The triangle ABC formed by AB = 5 cm, BC = 8 cm, AC = 4 cm is ______.
How many altitudes does a triangle have?
Which of the following figures will have it’s altitude outside the triangle?
The ______ triangle always has altitude outside itself.
Median is also called ______ in an equilateral triangle.
