Advertisements
Advertisements
Question
Draw an isosceles triangle. Draw all of its medians and altitudes. Write your observation about their points of concurrence.
Solution

Steps of construction:
- Draw an isosceles ∆XYZ.
- Draw the perpendicular bisector DE of the side YZ that intersect YZ at L.
- Join XL. XL is the median to side YZ.
- With X as centre and taking convenient radius, draw two arcs that intersect YZ at A and B.
- With A as centre and taking radius more than half of AB, draw an arc. With B as centre and taking same radius, draw another arc that cut the previous arc at C.
- Join XC that intersect YZ at L. XL is the altitude to the side YZ.
- Draw the perpendicular bisector IJ of the side ZX that intersect ZX at K.
- Join YK. YK is the median to side ZX.
- With Y as centre and taking convenient radius, draw two arcs that intersect ZX at Z and F.
- With Z as centre and taking radius more than half of ZF, draw an arc. With F as centre and taking same radius, draw another arc that cut the previous arc at H.
- Join YH that intersects ZX at M. YM is the altitude to the side ZX.
- Draw the perpendicular bisector ST of the side XY that intersects XY at U.
- Join ZU. ZU is the median to side XY.
- With Z as centre and taking a convenient radius, draw two arcs that intersect XY at P and Q.
- With P as centre and taking radius more than half of PQ, draw an arc. With Q as the center and taking the same radius, draw another arc that cuts the previous arc at R.
- Join ZR that intersects XY at N. ZN is the altitude to the side XY.
Hence, ∆XYZ is the required triangle in which the medians XL, YK and ZU to the sides YZ, ZX and XY respectively intersect at G and altitudes XL, YM and ZN to the sides YZ, ZX and XY respectively intersect at O. The point G is the centroid and point O is the orthocentre of ∆XYZ. We observe that, in an isosceles triangle, the points of concurrence of medians (centroid) and altitudes (orthocentre) lie on the same straight line.
RELATED QUESTIONS
In the given figure, point S is any point on side QR of ΔPQR Prove that: PQ + QR + RP > 2PS
Draw an obtuse angled Δ STV. Draw its medians and show the centroid.
Draw an obtuse angled Δ LMN. Draw its altitudes and denote the orthocentre by ‘O’.
The centroid of a triangle divides each medians in the ratio _______
The centroid, orthocentre, and incentre of a triangle are collinear
Identify the centroid of ∆PQR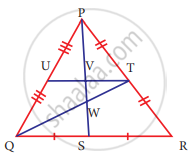
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If DE = 44, then DM = ?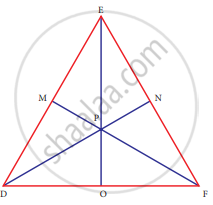
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If PD = 12, then PN = ?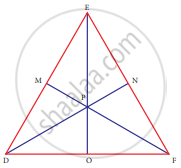
In ∆ABC, AD is the bisector of ∠A meeting BC at D, CF ⊥ AB and E is the mid-point of AC. Then median of the triangle is ______.
If we join a vertex to a point on opposite side which divides that side in the ratio 1:1, then what is the special name of that line segment?
