Advertisements
Advertisements
Question
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If PD = 12, then PN = ?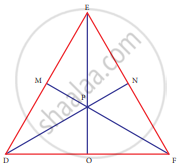
Solution
Given DN, EO, FM are medians.
∴ FN = EN
DO = FO
EM = DM
If PD = 12, PN = ?
`"PD"/"PN" = 2/1`
`12/"PN" = 2/1`
⇒ PN = `12/2` = 6
PN = 6
APPEARS IN
RELATED QUESTIONS
In ΔPQR, ∠Q = 90°, PQ = 12, QR = 5 and QS is a median. Find l(QS).
Draw an obtuse angled Δ LMN. Draw its altitudes and denote the orthocentre by ‘O’.
Draw an isosceles triangle. Draw all of its medians and altitudes. Write your observation about their points of concurrence.
The centroid, orthocentre, and incentre of a triangle are collinear
Identify the centroid of ∆PQR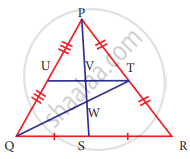
In the given figure, A is the midpoint of YZ and G is the centroid of the triangle XYZ. If the length of GA is 3 cm, find XA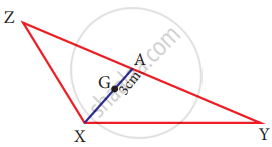
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If DE = 44, then DM = ?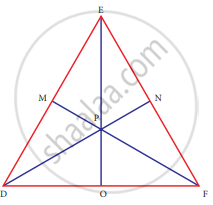
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If DO = 8, then FD = ?
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If OE = 36 then EP = ?
In ∆ABC, AD is the bisector of ∠A meeting BC at D, CF ⊥ AB and E is the mid-point of AC. Then median of the triangle is ______.
