Advertisements
Advertisements
Question
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If OE = 36 then EP = ?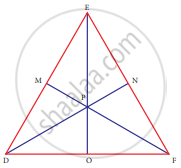
Solution
Given DN, EO, FM are medians.
∴ FN = EN
DO = FO
EM = DM
If OE = 36
then `"EP"/"PO" = 2/1`
`"EP"/2` = PO
OE = OP + PE
36 = `"PE"/2 + "PE"`
36 = `"PE"/2 + (2"PE")/2`
36 = `(3"PE")/2`
PE = `(36 xx 2)/3`
PE = 24
APPEARS IN
RELATED QUESTIONS
The length of hypotenuse of a right angled triangle is 15. Find the length of median of its hypotenuse.
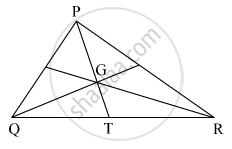
In the given figure, point G is the point of concurrence of the medians of Δ PQR. If GT = 2.5, find the lengths of PG and PT.
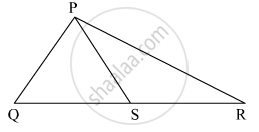
In the given figure, point S is any point on side QR of ΔPQR Prove that: PQ + QR + RP > 2PS
Draw an obtuse angled Δ STV. Draw its medians and show the centroid.
Draw an obtuse angled Δ LMN. Draw its altitudes and denote the orthocentre by ‘O’.
The centroid of a triangle divides each medians in the ratio _______
The centroid, orthocentre, and incentre of a triangle are collinear
Identify the centroid of ∆PQR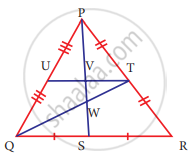
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If PD = 12, then PN = ?
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If DO = 8, then FD = ?
