Advertisements
Advertisements
Question
In the given figure, point G is the point of concurrence of the medians of Δ PQR. If GT = 2.5, find the lengths of PG and PT.
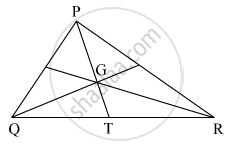
Solution
GT = 2.5 ...(Given)
The point of concurrence of medians of a triangle divides each median in the ratio 2 : 1.
∴ `"PG"/"GT" = 2/1`
∴ `"PG"/2.5 = 2/1`
∴ PG = 2 × 2.5
∴ PG = 5
Now, PT = PG + GT
= 5 + 2.5
∴ PT = 7.5 units
Hence, the length of PG and PT is 5 and 7.5 units respectively.
APPEARS IN
RELATED QUESTIONS
The length of hypotenuse of a right angled triangle is 15. Find the length of median of its hypotenuse.
In ΔPQR, ∠Q = 90°, PQ = 12, QR = 5 and QS is a median. Find l(QS).
Draw an obtuse angled Δ STV. Draw its medians and show the centroid.
Draw an obtuse angled Δ LMN. Draw its altitudes and denote the orthocentre by ‘O’.
The medians of a triangle cross each other at _______
In any triangle the centroid and the incentre are located inside the triangle
The centroid, orthocentre, and incentre of a triangle are collinear
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If DE = 44, then DM = ?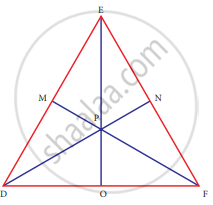
In ∆ABC, AD is the bisector of ∠A meeting BC at D, CF ⊥ AB and E is the mid-point of AC. Then median of the triangle is ______.
If we join a vertex to a point on opposite side which divides that side in the ratio 1:1, then what is the special name of that line segment?
