Advertisements
Advertisements
Question
Draw equipotential surfaces:
(1) in the case of a single point charge and
(2) in a constant electric field in Z-direction. Why are the equipotential surfaces about a single charge not equidistant?
(3) Can electric field exist tangential to an equipotential surface? Give reason
Solution
(1)
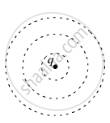
(2)

The equipotential surfaces about a single charge are not equidistant because electric field due to a single change is not constant.
(3) If the electric field exist along tangential to an equipotential surface, a charged particle will experience a force along the tangential line and can move along it. As a charged particle can move only due to the potential difference (along with the direction of change of potential), this contradicts the concept of an equipotential surface.
APPEARS IN
RELATED QUESTIONS
Define an equipotential surface.
A man fixes outside his house one evening a two metre high insulating slab carrying on its top a large aluminium sheet of area 1 m2. Will he get an electric shock if he touches the metal sheet next morning?
What is the geometrical shape of equipotential surfaces due to a single isolated charge?
Depict the equipotential surfaces for a system of two identical positive point charges placed a distance(d) apart?
Define equipotential surface.
Answer the following question.
Two identical point charges, q each, are kept 2m apart in the air. A third point charge Q of unknown magnitude and sign is placed on the line joining the charges such that the system remains in equilibrium. Find the position and nature of Q.
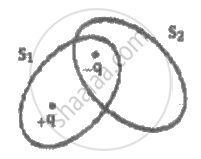
S1 and S2 are the two imaginary surfaces enclosing the charges +q and -q as shown. The electric flux through S1 and S2 are respectively ______.
The diagrams below show regions of equipotentials.
(i) |
(ii)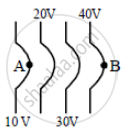 |
(iii) |
(iv) |
A positive charge is moved from A to B in each diagram.
Which of the following is NOT the property of equipotential surface?
Draw equipotential surfaces for (i) an electric dipole and (ii) two identical positive charges placed near each other.
