Advertisements
Advertisements
Questions
Draw the graphs of the equations 5x − y = 5 and 3x − y = 3. Determine the coordinates of the vertices of the triangle formed by these lines and the y axis.
Draw the graphs of the equations 5x − y = 5 and 3x − y = 3. Determine the coordinates of the vertices of the triangle formed by these lines and y-axis. Calculate the area of the triangle so formed.
Solution
The given equations are:
5x − y = 5 ........(i)
3x − y = 3 ...........(ii)
Putting x = 0 in equation (i) we get
`=> 5 xx 0 - y = 5`
`=> y = -5`
x = 0, y = -5
Putting y = 0 in eqaution (i) we get
=> 5x - 0 = 5
=> x = 1
x = 1, y = 0
Use the following table to draw the graph.
| x | 0 | 1 |
| y | -5 | 0 |
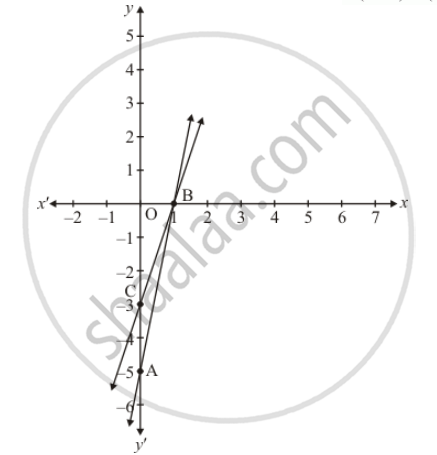
Draw the graph by plotting the two points A(0, -5), B(1, 0) from table
3x - y = 3 ....(ii)
Putting x = 0 in eqaution (ii) we get
`=> 3xx0-y = 3`
`=> y = -3``
`x= 0, y = -3`
Putting y = 0 in equation (ii) we get
`=> 3x - 0 = 3`
`=> x = 1`
x = 1, y = 0
Use the following table to draw the graph.
| x | 0 | 1 |
| y | -3 | 0 |
Draw the graph by plotting the two points C(0, -3), D(1,0) from table.
Hence the vertices of the required triangle are B(1,0), C(0, -3) and A(0, -5).
Now,
Required area = Area of PCA
Required area = 1/2 (base x height)
Required area = 1/2 (2 x 1) sq.units
Hence the required area is 1 sq units
APPEARS IN
RELATED QUESTIONS
Solve `\frac{1}{x+y}+\frac{2}{x-y}=2\text{ and }\frac{2}{x+y}-\frac{1}{x-y}=3` where, x + y ≠ 0 and x – y ≠ 0
Solve the following pairs of equations by reducing them to a pair of linear equations
`10/(x+y) + 2/(x-y) = 4`
`15/(x+y) - 5/(x-y) = -2`
The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.
The sum of two numbers is 8. If their sum is four times their difference, find the numbers.
The sum of digits of a two number is 15. The number obtained by reversing the order of digits of the given number exceeds the given number by 9. Find the given number.
The sum of two numbers is 1000 and the difference between their squares is 256000. Find the numbers.
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
If the numerator is multiplied by 2 and the denominator is reduced by 5, the fraction becomes `6/5`. Thus, we have
`(2x)/(y-5)=6/5`
`⇒ 10x=6(y-5)`
`⇒ 10x=6y-30`
`⇒ 10x-6y+30 =0`
`⇒ 2(5x-3y+15)=0`
`⇒ 5x - 3y+15=0`
If the denominator is doubled and the numerator is increased by 8, the fraction becomes `2/5`. Thus, we have
`(x+8)/(2y)=2/5`
`⇒ 5(x+8)=4y`
`⇒ 5x+40=4y`
`⇒ 5x-4y+40=0`
So, we have two equations
`5x-3y+15=0`
`5x-4y+40=0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
`x/((-3)xx40-(-4)xx15)=-y/(5xx40-5xx15)=1/(5xx(-4)-5xx(-3))`
`⇒ x/(-120+60)=(-y)/(200-75)=1/(-20+15)`
`⇒x/(-60)=-y/125``=1/-5`
`⇒ x= 60/5,y=125/5`
`⇒ x=12,y=25`
Hence, the fraction is `12/25`
The sum of the numerator and denominator of a fraction is 3 less than twice the denominator. If the numerator and denominator are decreased by 1, the numerator becomes half the denominator. Determine the fraction.
The sum of the numerator and denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes 1/2. Find the fraction.
Asha has only ₹1 and ₹2 coins with her. If the total number of coins that she has is 50 and the amount of money with her is ₹75, then the number of ₹1 and ₹2 coins are, respectively.
