Advertisements
Advertisements
Question
Draw the graph of the following function:
f(x) = `|x|/x`
Solution
If f: R → R is defined by
f(x) = `{(|x|/x if x ≠ 0),(0 if x = 0):}`
= `{(x/x if x > 0),((- x)/x if x < 0):}`
= `{(1 if x > 0),(- 1 if x < 0):}`
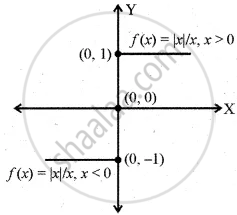
The domain of the function is R and the range is {-1, 0, 1}.
APPEARS IN
RELATED QUESTIONS
Determine whether the following function is odd or even?
f(x) = `log (x^2 + sqrt(x^2 + 1))`
Let f be defined by f(x) = x3 – kx2 + 2x, x ∈ R. Find k, if ‘f’ is an odd function.
If f(x) = ex and g(x) = loge x then find (f + g)(1)
Draw the graph of the following function:
f(x) = 16 – x2
Draw the graph of y = 9 - x2.
If f(x) = x2 – x + 1 then f(x + 1) is:
The graph of the line y = 3 is
The minimum value of the function f(x) = |x| is:
f(x) = -5, for all x ∈ R is a:
The range of f(x) = |x|, for all x ∈ R is:
