Advertisements
Advertisements
Question
Each student in a class of 35 plays atleast one game among chess, carrom and table tennis. 22 play chess, 21 play carrom, 15 play table tennis, 10 play chess and table tennis, 8 play carrom and table tennis and 6 play all the three games. Find the number of students who play only chess (Hint: Use Venn diagram)
Solution
Let A, B and C represent students play chess, carrom and table tennis.
n(A) = 22, n(B) = 21, n(C) = 15
n(A ∩ C) = 10, n(B ∩ C) = 8, n(A ∩ B ∩ C) = 6
Let “x” represent student play chess and carrom but not table tennis.
Let us represent the data in Venn diagram.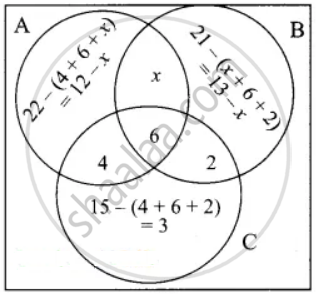
From the Venn diagram we get,
Number of students play atleast one game = 35
12 – x + x + 13 – x + 2 + 6 + 4 + 3 = 35
40 – 35 = x
5 = x
Number of students who play only chess
= 12 – x
= 12 – 5
= 7
APPEARS IN
RELATED QUESTIONS
State, whether the pair of sets, given below, are equal sets or equivalent sets:
{5, 5, 2, 4} and {5, 4, 2, 2}
State, whether the pair of sets, given below, are equal sets or equivalent sets:
{2, 4, 6, 8, 10} and {a, b, d, e, m}
Write the cardinal number of the following set:
B = {-3, -1, 1, 3, 5, 7}
Write the cardinal number of the following set:
C = { }
Given:
A = {Natural numbers less than 10}
B = {Letters of the word ‘PUPPET’}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by 2}.
Find: n(C)
State true or false for the following. Correct the wrong statement.
n(Φ) = 1
In a class, all students take part in either music or drama or both. 25 students take part in music, 30 students take part in drama and 8 students take part in both music and drama. Find the number of students who take part in only music
In a party of 45 people, each one likes tea or coffee or both. 35 people like tea and 20 people like coffee. Find the number of people who like both tea and coffee
In an examination 50% of the students passed in Mathematics and 70% of students passed in Science while 10% students failed in both subjects. 300 students passed in both the subjects. Find the total number of students who appeared in the examination, if they took examination in only two subjects
For any three sets A, B and C, (A – B) ∩ (B – C) is equal to
