Advertisements
Advertisements
Question
Each student in a class of 35 plays atleast one game among chess, carrom and table tennis. 22 play chess, 21 play carrom, 15 play table tennis, 10 play chess and table tennis, 8 play carrom and table tennis and 6 play all the three games. Find the number of students who play only carrom (Hint: Use Venn diagram)
Solution
Let A, B and C represent students play chess, carrom and table tennis.
n(A) = 22, n(B) = 21, n(C) = 15
n(A ∩ C) = 10, n(B ∩ C) = 8, n(A ∩ B ∩ C) = 6
Let “x” represent student play chess and carrom but not table tennis.
Let us represent the data in Venn diagram.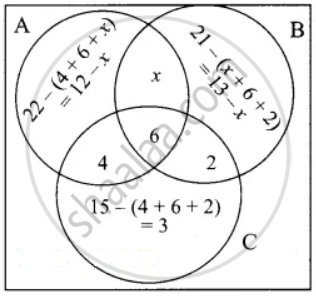
From the Venn diagram we get,
Number of students play atleast one game = 35
12 – x + x + 13 – x + 2 + 6 + 4 + 3 = 35
40 – 35 = x
5 = x
Number of students who play only carrom
= 13 – x
= 13 – 5
= 8
APPEARS IN
RELATED QUESTIONS
State, whether the pair of sets, given below, are equal sets or equivalent sets:
{8, 6, 10, 12} and {3, 2, 4, 6}
Write the cardinal number of the following set:
A = {0, 1, 2, 4}
Write the cardinal number of the following set:
F = {Whole numbers from 8 to 14}
Given:
A = {Natural numbers less than 10}
B = {Letters of the word ‘PUPPET’}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by 2}.
Find: n(C)
Given:
A = {Natural numbers less than 10}
B = {Letters of the word ‘PUPPET’}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by 2}.
Find: A ∩ C AND n(A ∩ C)
In a class, all students take part in either music or drama or both. 25 students take part in music, 30 students take part in drama and 8 students take part in both music and drama. Find the number of students who take part in only music
Out of 500 car owners investigated, 400 owned car A and 200 owned car B, 50 owned both A and B cars. Is this data correct?
In the adjacent diagram, if n(U) = 125, y is two times of x and z is 10 more than x, then find the value of x, y and z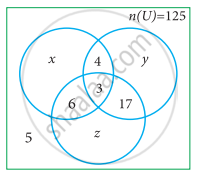
If n(A ∪ B ∪ C) = 100, n(A) = 4x, n(B) = 6x, n(C) = 5x, n(A ∩ B) = 20, n(B ∩ C) = 15, n(A ∩ C) = 25 and n(A ∩ B ∩ C) = 10, then the value of x is
In a city, 40% people like only one fruit, 35% people like only two fruits, 20% people like all the three fruits. How many percentage of people do not like any one of the above three fruits?
