Advertisements
Advertisements
Question
एक बहुफलकी में 10 फलक, 20 किनारे और 15 शीर्ष हो सकते हैं।
Options
सत्य
असत्य
Solution
यह कथन असत्य है।
स्पष्टीकरण -
हम जानते हैं कि, आयलर का सूत्र प्रत्येक बहुफलक के लिए संतुष्ट करता है।
यानी F + V – E = 2
यहाँ, F = 10, E = 20
और V = 15
इन मानों को आयलर के सूत्र में रखने पर, हमें प्राप्त होता है।
10 + 15 – 20 = 2
⇒ 25 – 20 = 2
⇒ 5 ≠ 2
अतः, दिए गए मान आयलर के सूत्र को संतुष्ट नहीं करते।
APPEARS IN
RELATED QUESTIONS
निम्न में से कौन एक सम बहुफलकी है?
एक बहुफलकी में, यदि F = V = 5 है, तो इस आकार में किनारों की संख्या होगी -
निम्न में से कौन एक बहुफलकी के लिए सत्य नहीं हो सकता?
यदि किसी बहुफलकी के 12 फलक और 20 शीर्ष हैं, तो इस ठोस में किनारों की संख्या ______ है।
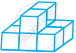में घनों की संख्या ______ है।
यदि एक बहुफलकी में शीर्षो और फलकों की संख्याओं का योग 14 है, तो इस आकार में किनारों की संख्या ______ है।
निम्न आकारों को देखिए और बताइए कि इनमें कौन-कौन बहुफलकी हैं।
निम्न आकारों को देखिए और बताइए कि इनमें कौन-कौन बहुफलकी हैं।
निम्न आकारों को देखिए और बताइए कि इनमें कौन-कौन बहुफलकी हैं।
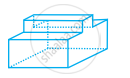
एक बहुफलकी में 40 फलक और 60 किनारे हैं। इस ठोस के शीषों की संख्या ज्ञात कीजिए।
