Advertisements
Advertisements
Question
एक बक्से में 8 लाल गेंद तथा कुछ नीली गेंदें हैं। यादृच्छिक पद्घति से बक्से में से एक गेंद निकालनी है। लाल गेंद तथा नीली गेंद निकालने की संभाव्यता का अनुपात 2 : 5 है। नीली गेंदों की संख्या ज्ञात करो।
Solution
मानो, नीली गेंदों की संख्या x है।
तब, ∴ n(B) = x
लाल गेंदों की संख्या 8 है।
कुल गेंदों की संख्या = x + 8
∴ n(S) = x + 8
नीली गेंद प्राप्त होने की संभाव्यता,
P(B) = `(n(B))/(n(S))`
∴ P(B) = `x/(x + 8)`
लाल गेंद प्राप्त होने की संभाव्यता,
P(R) = `(n(R))/(n(S))`
∴ P(R) = `x/(x + 8)`
दी गई शर्त ते अनुसार,
`(P(R))/(P(B)) = 2/5`
∴ `8/(x + 8) ÷ x/(x + 8) = 2/5`
∴ `8/(x + 8) xx (x + 8)/x = 2/5`
∴ `8/x = 2/5`
∴ 8 × 5 = 2 × x
∴ x = `(8 xx 5)/2`
∴ x = 20
नीली गेंदों की संख्या 20 है।
APPEARS IN
RELATED QUESTIONS
दो सिक्के को उछालने पर निम्नलिखित घटनाओं की संभाव्यता ज्ञात कीजिए।
एक भी चित न मिलना।
दो पाँसे एक ही समय फेंकने पर निम्नलिखित घटनाओं की संभाव्यता ज्ञात कीजिए।
पृष्ठभागों पर आने वाली संख्याओं का योगफल कम-से-कम 10 है।
दो पाँसे एक ही समय फेंकने पर निम्नलिखित घटनाओं की संभाव्यता ज्ञात कीजिए।
पृष्ठभागों पर आने वाली संख्याओं का योगफल 33 है।
अंकों की पुनरावृत्ति न करते हुए 2, 3, 5, 7, 9 अंकों से दो अंकों वाली संख्या बनायी गई हो तो निम्नलिखित घटनाओं की संभाव्यता ज्ञात कीजिए।
वह संख्या विषम हो।
एक बक्से मेंं 5 लाल पेन, 8 नीली पेन और 3 हरी पेन है। यादृच्छिक पद्धति से ऋतुजा को एक पेन निकालना है। तो उस पेन के नीला होने की संभाव्यता ज्ञात करो।
संयोग के खेल मेंं 1, 2, 3, 4, 5, 6, 7, 8 मेंं से किसी एक अंक पर तीर स्थिर होता है और यह समसंभाव्यता का फल है। तो निम्न घटनाओं की संभाव्यता ज्ञात कीजिए।
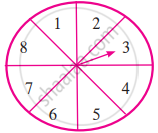
- वह तीर 8 अंक पर स्थिर होगा।
- वह तीर विषम अंक पर स्थिर होगा।
- तीर से दर्शाई गई संख्या 2 से बड़ी होगी।
- तीर से दर्शाई गई संख्या 9 से छोटी होगी।
प्रत्येक कार्डपर एक इस प्रकार से 0 से 5 यह पूर्णांक संख्याएँ लिखकर बने छह कार्ड बक्से मेंं रखे गए हैं। निम्नलिखित प्रत्येक घटनाओं की संभाव्यता ज्ञात कीजिए।
निकाले गए कार्ड की संख्या पूर्ण संख्या हो।
निम्नलिखित कृति पूर्ण कीजिए।
नमूना अवकाश स्वयं निश्चित करके निम्नलिखित चौखट भरें।
| नमूना अवकाश | घटना A के लिए शर्त है कि संख्या ‘सम’ हो। |
| ↓ | ↓ |
| S = { } | A = { } |
| ↓ | ↓ |
| n(S) = `square` | n(A) = `square` |
P(A) = `square/square = square`
एक पाँसा फेंका गया। ऊपरी पृष्ठभाग पर आने वाली संख्या अभाज्य हो, तो इस घटना की संभाव्यता ज्ञात करने के लिए निम्न कृति को पूर्ण करो:
कृति:
एक पाँसा फेंका गया। नमूना अवकाश ‘S’ है।
S = `{square}`
∴ n(S) = 6
घटना A: ऊपरी पृष्ठभाग पर अभाज्य संख्या हो।
A = `{square}`
∴ n(A) = 3
P(A) = `square/(n(S))`
∴ P(A) = `square`
एक सिक्का तथा एक पाँसा एक साथ उछाले गये, तो निम्न घटना की संभाव्यता ज्ञात कीजिये:
घटना B: पट तथा विषम संख्या मिलना।
