Advertisements
Advertisements
Question
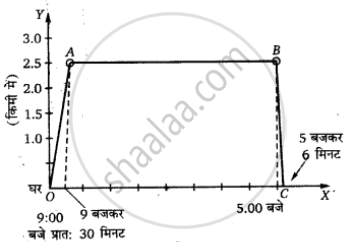
एक महिला अपने घर से प्रातः 9.00 बजे 2.5 km दूर अपने कार्यालय के लिए सीधी सड़क पर 5 kmh-1 चाल से चलती है। वहाँ वह सायं 5.00 बजे तक रहती है और 25 kmh-1 की चाल से चल रही किसी ऑटो रिक्शा द्वारा अपने घर लौट आती है। उपयुक्त पैमाना चुनिए तथा उसकी गति का x-t ग्राफ खींचिए।
Solution
महिला द्वारा घर से कार्यालय तक पहुँचने में लिया गया समय,
`"t"_1 = "दुरी" /"चाल" = (2.5 "किमी")/(5.0 "किमी"//"घंटा") = 1/2 "घंटा" = 0.5 "घंटा" = 30 "मिनट"`
महिला के कार्यालय पहुँचने का समय = 9.00 + 0.30 = 9.30 प्रातः
कार्यालय में ठहरने का समय = 9.30 प्रातः से 5.00 सायं
महिला द्वारा कार्यालय से घर तक वापस लौटने में लिया गया समय -
`"t"_2 = "दूरी"/"ऑटो रिक्शा की चाल"`
= `(2.5 "किमी")/(25 "किमी"//"घंटा")`
= `1/10 ` घंटा = 6 मिनट
महिला के घर पहुँचने का समय = 5.06 सायं
पैमाना- X-अक्ष पर: 10 खाने = 1 घंटा
Y-अक्ष पर: 20 खाने = 1 किमी
APPEARS IN
RELATED QUESTIONS
कोई जेट वायुयान 500 kmh-1 की चाल से चल रहा है और यह जेट यान के सापेक्ष 1500 kmh-1 की चाल से अपने दहन उत्पादों को बाहर निकालता है। जमीन पर खड़े किसी प्रेक्षक के सापेक्ष इन दहन उत्पादों की चाल क्या होगी?
दो नगर A व B नियमित बस सेवा द्वारा एक-दूसरे से जुड़े हैं और प्रत्येक T मिनट के बाद दोनों तरफ बसें चलती हैं। कोई व्यक्ति साइकिल से 20 kmh-1 की चाल से A से B की तरफ जा रहा है और यह नोट करता है कि प्रत्येक 18 मिनट के बाद एक बस उसकी गति की दिशा में तथा प्रत्येक 6 मिनट बाद उसके विपरीत दिशा में गुजरती है। बस सेवाकाल T कितना है और बसें सड़क पर किस चाल (स्थिर मानिए) से चलती हैं?
नीचे दिए गए कथन को ध्यान से पढिए और कारण बताते हुए व उदाहरण देते हुए बताइए कि वे सत्य हैं या असत्य:
एकविमीय गति में किसी कण की चाल शून्य होने पर भी उसका वेग अशून्य हो सकता है।
कोई व्यक्ति अपने घर से सीधी सड़क पर 5 kmh-1 की चाल से 2.5 km दूर बाजार तक पैदल जाता है। परंतु बाजार बंद देखकर वह उसी क्षण वापस मुड़ जाता है तथा 7.5 km h-1 की चाल से घर लौट आता है। समय अंतराल (i) 0-30 मिनट, (ii) 0-50 मिनट, (iii) 0-40 मिनट की अवधि में उस व्यक्ति (a) के माध्य वेग का परिमाण तथा (b) की माध्य चाल क्या है?
(नोट: आप इस उदाहरण से समझ सकेंगे कि औसत चाल को औसत-वेग के परिमाण के रूप में परिभाषित करने की अपेक्षा समय द्वारा विभाजित कुल पथ-लंबाई के रूप में परिभाषित करना अधिक अच्छा क्यों है? आप थककर घर लौटे उस व्यक्ति को यह बताना नहीं चाहेंगे कि उसकी औसत चाल शून्य थी।)
हमने अभ्यास में औसत चाल व औसत वेग के परिमाण के बीच के अंतर को स्पष्ट किया है। यदि हम तात्क्षणिक चाल व वेग के परिमाण पर विचार करते हैं तो इस तरह का अंतर करना आवश्यक नहीं होता। तात्क्षणिक चाल हमेशा तात्क्षणिक वेग के बराबर होती है। क्यों?
चित्र में दिखाए गए ग्राफ के लिए किसी उचित भौतिक स्थिति का सुझाव दीजिए: