Advertisements
Advertisements
Question
एक सर्वसम भारी झूलते पुल की केबिल (cable) परवलय के रूप में लटकी हुई है। सड़क पथ जो क्षैतिज है 100 मीटर लंबा है तथा केबिल से जुड़े ऊर्ध्वाधर तारों पर टिका हुआ है, जिसमें सबसे लंबा तार 30 मीटर और सबसे छोटा तार 6 मीटर है। मध्य से 18 मीटर दूर सड़क पथ से जुड़े समर्थक (supporting) तार की लंबाई ज्ञात कीजिए।
Solution
मान लीजिए AOB सर्वसम भारी झूलते पुल की केबिल है। माना कि AL और BM सबसे लंबे तार हैं, प्रत्येक की लंबाई 30 मीटर है। माना OC 6 मीटर लंबाई का सबसे छोटा तार है और LM सड़क पथ है।
अब AL = BM = 30 मीटर, OC = 6 मीटर और LM = 100 मीटर
∴ LC = CM = `1/2` LM = 50 मीटर
माना कि O शीर्ष है और परवलय का अक्ष y-अक्ष है। तो, मानक रूप में परवलय का समीकरण x2 = 4ay है
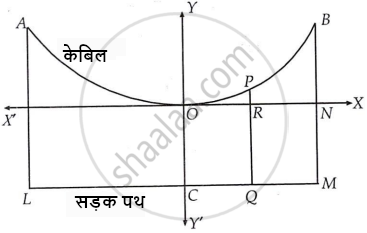
बिंदु B के निर्देशांक (50, 24) हैं
चूँकि बिंदु B परवलय पर स्थित है, x2 = 4ay
∴ (50)2 = 4a × 24
⇒ a = `2500/(4 xx 24)`
= `625/6`
तो, परवलय का समीकरण है
x2 = `(4 xx 625)/24 y` = x2 = `625/6 y`
माना 18 मीटर की दूरी पर सहायक तार PQ की लंबाई h है।
∴ OR = 18 मीटर और PR = PQ - QR = h - 6.
बिंदु P के निर्देशांक (18, h - 6) हैं
चूँकि बिंदु P परवलय x2 = `625/6 y` पर स्थित है
∴ (18)2 = `625/6 (h - 6)`
= 324 × 6 = 625h - 3750
= 625h = 1944 + 3750
= h = `5694/625`
तार की लंबाई = 9.11 मीटर लगभग.
APPEARS IN
RELATED QUESTIONS
निम्नलिखित प्रश्न में परवलय का समीकरण ज्ञात कीजिए जो दिए प्रतिबंध को संतुष्ट करता है:
नाभि (6, 0), नियता x = –6
निम्नलिखित प्रश्न में परवलय का समीकरण ज्ञात कीजिए जो दिए प्रतिबंध को संतुष्ट करता है:
नाभि (0, –3), नियता y = 3
निम्नलिखित प्रश्न में परवलय का समीकरण ज्ञात कीजिए जो दिए प्रतिबंध को संतुष्ट करता है:
शीर्ष (0, 0), नाभि (3, 0)
निम्नलिखित प्रश्न में परवलय का समीकरण ज्ञात कीजिए जो दिए प्रतिबंध को संतुष्ट करता है:
शीर्ष (0, 0), नाभि (−2, 0)
निम्नलिखित प्रश्न में परवलय का समीकरण ज्ञात कीजिए जो दिए प्रतिबंध को संतुष्ट करता है:
शीर्ष (0, 0), (2, 3) से जाता है और अक्ष, x-अक्ष के अनुदिश है।
निम्नलिखित प्रश्न में परवलय का समीकरण ज्ञात कीजिए जो दिए प्रतिबंध को संतुष्ट करता है:
शीर्ष (0, 0), (5, 2) से जाता है और y-अक्ष के सापेक्ष सममित है।
निम्नलिखित प्रश्न में, दिए प्रतिबंधों को संतुष्ट करते हुए दीर्घवृत्त का समीकरण ज्ञात कीजिए:
नाभियाँ (±3, 0), a = 4
निम्नलिखित प्रश्न में, दिए प्रतिबंधों को संतुष्ट करते हुए दीर्घवृत्त का समीकरण ज्ञात कीजिए:
b = 3, c = 4, केंद्र मूल बिंदु पर, नाभियाँ x-अक्ष पर है।
निम्नलिखित प्रश्न में, दिए प्रतिबंधों को संतुष्ट करते हुए दीर्घवृत्त का समीकरण ज्ञात कीजिए:
केंद्र (0, 0) पर, दीर्घ अक्ष y-अक्ष पर और बिंदुओं (3, 2) और (1, 6) से जाता है।
निम्नलिखित प्रश्न में, दिए प्रतिबंधों को संतुष्ट करते हुए दीर्घवृत्त का समीकरण ज्ञात कीजिए:
दीर्घ अक्ष,x-अक्ष पर और बिंदुओं (4, 3), (6, 2) से जाता है।
यदि एक परवलयाकार परावर्तक का व्यास 20 सेमी और गहराई 5 सेमी है। नाभि ज्ञात कीजिए।
एक मेहराब परवलय के आकार का है और इसका अक्ष ऊर्ध्वाधर है। मेहराब 10 मीटर ऊँचा है और आधार में 5 मीटर चौड़ा है। यह, परवलय के दो मीटर की दूरी पर शीर्ष से कितना चौड़ा होगा?
परवलय y2 = 4ax, के अंतर्गत एक समबाहु त्रिभुज है जिसका एक शीर्ष परवलय का शीर्ष है। त्रिभुज की भुजा की लंबाई ज्ञात कीजिए।
