Advertisements
Advertisements
Question
एक वर्गांकित शीट पर, बराबर क्षेत्रफलों वाले दो त्रिभुजों को इस प्रकार बनाइए कि त्रिभुज सर्वांगसम न हों।
आप उनके परिमाप के बारे में क्या कह सकते हैं?
Solution
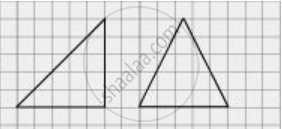
यहाँ, दो त्रिभुजों की ऊँचाई और आधार समान हैं। इस प्रकार, उनके क्षेत्र समान हैं। हालाँकि, ये त्रिभुज एक दूसरे के सर्वांगसम नहीं हैं। साथ ही, दोनों त्रिभुजों का परिमाप समान नहीं होगा।
APPEARS IN
RELATED QUESTIONS
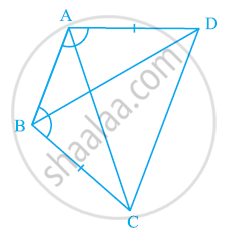
ABCD एक चतुर्भुज है, जिसमें AD = BC और ∠DAB = ∠CBA है (देखिए आकृति)। सिद्ध कीजिए कि:
- △ABD ≌ △BAC
- BD = AC
- ∠ABD = ∠BAC
यदि △DEF ≅ △BCA हो, तो △BCA के उन भागो को लिखिए जो ∠F के संगत हो:
निम्नलिखित में से कौन त्रिभुजों की सर्वांगसमता की एक कसौटी नहीं है?
यदि AB = QR, BC = PR और CA = PQ है, तो ______।
∆PQR में, ∠R = ∠P तथा QR = 4 cm और PR = 5 cm है, तब PQ की लम्बाई है
नीचे दिए गए उदाहरण में त्रिभुज की जोड़ियों के सर्वांगसम घटक एक जैसे चिह्न से दर्शाए गए हैं। प्रत्येक जोड़ी के त्रिभुज किस कसौटी के आधार पर सर्वांगसम हैं रिक्त स्थानों में वह कसौटी लिखिए।
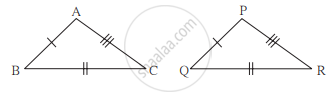
______ कसौटी से
ΔABC ≅ ΔPQR
नीचे दिए गए त्रिभु की जोड़ि में दर्शाई गई जानकारी का निरीक्षण कीजिए । वे त्रिभुज किस कसौटी के आधार पर सर्वांगसम हैं शेष सर्वांगसम घटक भी लिखिए ।
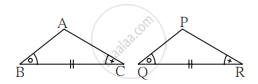
आकृति में दर्शाई गई जानकारी के आधार पर,
ΔABC तथा ΔPQR में
∠ABC ≅ ∠PQR
रेख BC ≅ रेख QR
∠ACB ≅ ∠PQR
∴ ΔABC ≅ ΔPQR........... `square` कसौटी
∴ ∠BAC ≅ `square` ....... सर्वांगसम त्रिभुजों के संगत कोण
रेख AB ≅ `square` तथा `square` ≅ रेख PR .....सर्वांगसम त्रिभुज की संगत भुजाएँ
नीचे दिए गए त्रिभुज की जोड़िय में दर्शाई गई जानकारी का निरीक्षण कीजिए । वे त्रिभुज किस कसौटी के आधार पर सर्वांगसम हैं । शेष सर्वांगसम घटक भी लिखिए ।
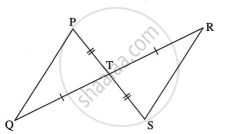
आकृति में दर्शाई गई जानकारी के आधार पर,
ΔPTQ तथा ΔSTR में
रेख PT ≅ रेख ST
∠PTQ ≅ ∠STR ...शीर्षाभिमुख कोण
रेख TQ ≅ रेख TR
∴ ΔPTQ ≅ ΔSTR .... `square` कसौटी
∴ `{:(∠"TPQ" ≅ square),(व square ≅ ∠"TRS"):}}` ...सर्वांगसम त्रिभुज के संगत कोण
रेख PQ ≅ `square` ...सर्वांगसम त्रिभुज की संगत भुजाएँ
नीचे दी गई आकृति में Δ ABC तथा Δ PQR की सर्वांगसमता की कसौटी लिखकर शेष सर्वांगसम घटकों के नाम लिखिए।
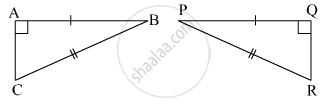
निचे दी गई आकृति के आधार पर ∠P ≅ ∠R, रेख PQ ≅ रेख QR, तो सिद्ध कीजिए कि, ΔPQT ≅ ΔRQT