Advertisements
Advertisements
Question
निम्नलिखित में से कौन त्रिभुजों की सर्वांगसमता की एक कसौटी नहीं है?
Options
SAS
ASA
SSA
SSS
Solution
SSA
स्पष्टीकरण -
हम वह जानते हैं,
दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज की भुजा (S) और कोण (A) दूसरे कोण के बराबर हों।
और त्रिभुज की सर्वांगसमता के मानदंड SAS, ASA, SSS और RHS हैं।
SSA त्रिभुज की सर्वांगसमता की कसौटी नहीं है।
APPEARS IN
RELATED QUESTIONS
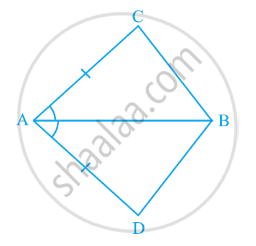
चतुर्भुज ABCD में, AC = AD है और AB, कोण A को समद्विभाजित करता है (देखिए आकृति)। दर्शाइए कि △ABC ≌ △ABD है। BC और BD के बारे में आप क्या कह सकते हैं?
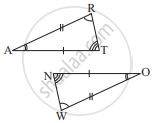
आकृति में दो त्रिभुज ART तथा OWN सर्वांगसम हैं जिसके संगत भागो को अंकित किया गया है। हम लिख सकते है △RAT ≅ ?
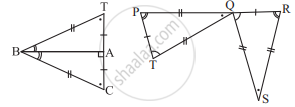
कथनों को पूरा कीजिए:
ΔBCA ≅?
∆QRS ≅ ?
∆ABC में, BC = AB और ∠B = 80° है, तब ∠A बराबर है
∆PQR में, यदि ∠R > ∠Q है, तो ______
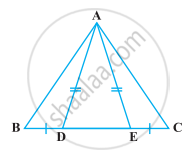
निम्नलिखित आकृति में, D और E त्रिभुज ABC की भुजा BC पर दो बिंदु इस प्रकार स्थित हैं कि BD = CE और AD = AE है। दर्शाइए कि ∆ABD ≅ ∆ACE है।
नीचे दिए गए प्रत्येक उदाहरण में त्रिभुज की जोड़ि के सर्वांगसम घटक एक जैसे चिह्न से दर्शाए गए हैं। त्रिभुज किस कसौटी के आधार पर सर्वांगसम हैं रिक्त स्थानों में वह कसौटी लिखिए।
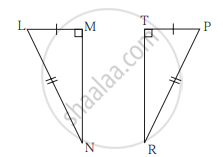
______ कसौटी से
ΔLMN ≅ ΔPTR
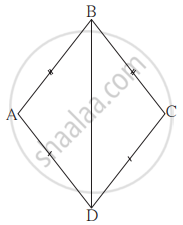
आकृति में रेख AB ≅ रेख BC तथा रेख AD ≅ रेख CD तो सिद्ध कीजिए Δ ABD ≅ Δ CBD
ΔTPQ में ∠T = 65°, ∠P = 95° तो निम्नलिखित में से कौन-सा कथन सत्य है ?
समद्विबाहु ΔABC में AB = AC है। BD तथा CE दो माध्यिकाएँ हैं तो सिद्ध कीजिए कि BD = CE
