Advertisements
Advertisements
Question
समद्विबाहु ΔABC में AB = AC है। BD तथा CE दो माध्यिकाएँ हैं तो सिद्ध कीजिए कि BD = CE
Solution

बिंदु D रेख AC का मध्यबिंदु है । ...(मध्यबिंदु की परिभाषा से)
∴ AD = DC = `1/2` AC ...(1)
AE = EB = `1/2`AB ....(2)
AB = AC
दोनों पक्षो में `1/2` से गुणा करने पर,
`1/2 "AB" = 1/2 "AC"` ...(3)
∴ AE = AD .....[(1), (2) तथा (3) से] ...(4)
ΔBAD तथा ΔCAE में,
रेख AB ≅ रेख AC ...(दिया है।)
∠BAD ≅ ∠CAE ...(सामान्य रूप)
रेख AE ≅ रेख AD ....(4 से)
∴ ΔBAD ≅ ΔCAE ....(सर्वांगसमता की भू - को - भू कसौटी से)
∴ रेख BD ≅ रेख CE
∴ BD = CE.
APPEARS IN
RELATED QUESTIONS
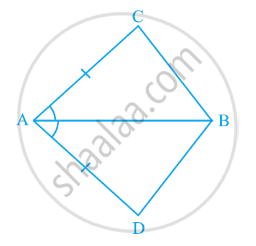
चतुर्भुज ABCD में, AC = AD है और AB, कोण A को समद्विभाजित करता है (देखिए आकृति)। दर्शाइए कि △ABC ≌ △ABD है। BC और BD के बारे में आप क्या कह सकते हैं?
यदि △DEF ≅ △BCA हो, तो △BCA के उन भागो को लिखिए जो ∠E के संगत हो:
यदि △DEF ≅ △BCA हो, तो △BCA के उन भागो को लिखिए जो `bar(DF)` के संगत हो:
∆ABC में, BC = AB और ∠B = 80° है, तब ∠A बराबर है
एक त्रिभुज की दो भुजाओं की लंबाइयाँ 5 cm और 1.5 cm हैं। इस त्रिभुज की तीसरी भुजा की लंबाई निम्नलिखित नहीं हो सकती ______
नीचे दिए गए उदाहरण में त्रिभुज की जोड़ियों के सर्वांगसम घटक एक जैसे चिह्न से दर्शाए गए हैं। प्रत्येक जोड़ी के त्रिभुज किस कसौटी के आधार पर सर्वांगसम हैं रिक्त स्थानों में वह कसौटी लिखिए।
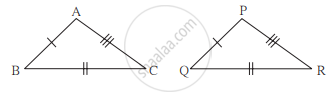
______ कसौटी से
ΔABC ≅ ΔPQR
नीचे दिए गए प्रत्येक उदाहरण में त्रिभुज की जोड़ि के सर्वांगसम घटक एक जैसे चिह्न से दर्शाए गए हैं। प्रत्येक जोड़ी के त्रिभुज किस कसौटी के आधार पर सर्वांगसम हैं रिक्त स्थानों में वह कसौटी लिखिए।

______ कसौटी से
ΔPRQ ≅ ΔSTU
नीचे दिए गए प्रत्येक उदाहरण में त्रिभुज की जोड़ि के सर्वांगसम घटक एक जैसे चिह्न से दर्शाए गए हैं। त्रिभुज किस कसौटी के आधार पर सर्वांगसम हैं रिक्त स्थानों में वह कसौटी लिखिए।
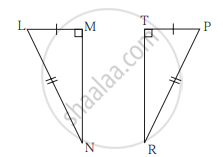
______ कसौटी से
ΔLMN ≅ ΔPTR
नीचे दिए गए त्रिभु की जोड़ि में दर्शाई गई जानकारी का निरीक्षण कीजिए । वे त्रिभुज किस कसौटी के आधार पर सर्वांगसम हैं शेष सर्वांगसम घटक भी लिखिए ।
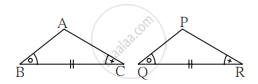
आकृति में दर्शाई गई जानकारी के आधार पर,
ΔABC तथा ΔPQR में
∠ABC ≅ ∠PQR
रेख BC ≅ रेख QR
∠ACB ≅ ∠PQR
∴ ΔABC ≅ ΔPQR........... `square` कसौटी
∴ ∠BAC ≅ `square` ....... सर्वांगसम त्रिभुजों के संगत कोण
रेख AB ≅ `square` तथा `square` ≅ रेख PR .....सर्वांगसम त्रिभुज की संगत भुजाएँ
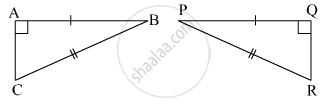
नीचे दी गई आकृति में Δ ABC तथा Δ PQR की सर्वांगसमता की कसौटी लिखकर शेष सर्वांगसम घटकों के नाम लिखिए।